 por leticiapires52 » Sex Fev 13, 2015 11:20
por leticiapires52 » Sex Fev 13, 2015 11:20
-
leticiapires52
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Qua Fev 12, 2014 10:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por Baltuilhe » Sex Fev 13, 2015 14:47
por Baltuilhe » Sex Fev 13, 2015 14:47
Leticia, boa tarde!
Esta função é DESCONTÍNUA, pois:
Limite à esquerda de -2:
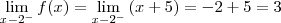
Limite à direita de -2:
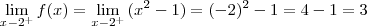
Portanto:
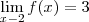
Então, limites à esquerda e à direita existem e SÃO iguais, portanto, existe o limite.
Mas para a função ser contínua além do limite existir a função deve existir no ponto e possuir MESMO valor que o obtido pelos limites laterais.
No caso a função possui valor no ponto onde x=-2.
Pela definição passada:
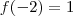
Mas como 1 é diferente de 3, a função é DESCONTÍNUA.
Espero ter ajudado!
-
Baltuilhe
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Dom Mar 24, 2013 21:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- função descontinua
por alexandreredefor » Seg Jul 18, 2011 17:50
- 2 Respostas
- 2842 Exibições
- Última mensagem por LuizAquino

Ter Jul 19, 2011 17:31
Cálculo: Limites, Derivadas e Integrais
-
- Função descontinua alguém pode me ajudar
 por Marcia C Silva » Sáb Mai 28, 2016 22:43
por Marcia C Silva » Sáb Mai 28, 2016 22:43
- 1 Respostas
- 1892 Exibições
- Última mensagem por nakagumahissao

Dom Mai 29, 2016 22:09
Funções
-
- Explique porque a função é descontínua no numero dado
por Pedro Coin » Sex Mai 27, 2016 23:20
- 1 Respostas
- 2651 Exibições
- Última mensagem por nakagumahissao

Dom Mai 29, 2016 22:10
Cálculo: Limites, Derivadas e Integrais
-
- Função continua
por Amparo » Dom Mar 09, 2008 16:14
- 1 Respostas
- 3931 Exibições
- Última mensagem por admin

Qui Mar 13, 2008 12:52
Funções
-
- função continua
por alexandreredefor » Dom Jul 17, 2011 18:23
- 4 Respostas
- 3201 Exibições
- Última mensagem por Molina

Seg Jul 18, 2011 11:42
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



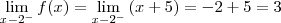
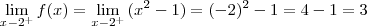
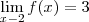
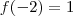

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.