Tenho um exemplo resolvido pelo professor que me deixou ainda mais confuso:
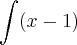
No caso dessa integral simples ele resolveu por partes usando: u = x - 1 e dx = dv, até ai beleza...mas o que eu não entendo é porquê eu não posso fazer por substituição usando u = x - 1 e du = dx daí eu teria
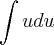 que é mais fácil de resolver.
que é mais fácil de resolver.


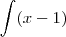
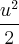 >>>
>>> 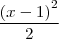 + C >>>
+ C >>> 
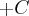
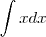 >>>
>>> 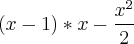 + C >>>
+ C >>> 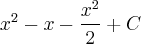
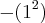
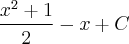
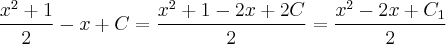
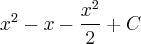
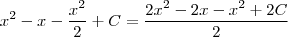
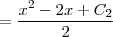
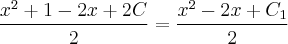
 saiu ?
saiu ?![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)