 por neoreload » Qua Fev 04, 2015 05:50
por neoreload » Qua Fev 04, 2015 05:50
Pessoal eu tava fazendo um exercício e só falta simplificar, mas isso n consegui fazer:
Simplificar:
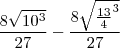
Resposta:
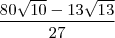
Na parte da raiz quadrada de 10 elevado a 3, da até pra ter uma certa noção, agora no 13/4 elevado a 3 eu não tenho nem ideia de como virou o 13 raiz de 13.
-
neoreload
- Usuário Dedicado

-
- Mensagens: 27
- Registrado em: Sáb Ago 09, 2014 16:15
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Russman » Qua Fev 04, 2015 18:25
por Russman » Qua Fev 04, 2015 18:25

O 8 no denominador simplifica o 8 da expressão. Faça o mesmo para
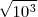
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por neoreload » Sáb Fev 07, 2015 22:10
por neoreload » Sáb Fev 07, 2015 22:10
adauto martins escreveu:![8/27(\sqrt[]{10.{10}^{2}}-\sqrt[]{(13/4).({13/4})^{2}}) 8/27(\sqrt[]{10.{10}^{2}}-\sqrt[]{(13/4).({13/4})^{2}})](/latexrender/pictures/fb741cbfcaceae43ba30ef2b3a01bbff.png)
=
![8/27(10.\sqrt[]{10}-(13/4)\sqrt[]{13/4})=8/27(10.\sqrt[]{10}-13/8\sqrt[]{13}=(80.\sqrt[]{10}-13\sqrt[]{13})/27 8/27(10.\sqrt[]{10}-(13/4)\sqrt[]{13/4})=8/27(10.\sqrt[]{10}-13/8\sqrt[]{13}=(80.\sqrt[]{10}-13\sqrt[]{13})/27](/latexrender/pictures/0f946dc3a762606c140e2c19fbe20087.png)
Amigo entendi quase tudo, no caso na parte do
![8/27(10\sqrt[]{10}-13/8\sqrt[]{13}) 8/27(10\sqrt[]{10}-13/8\sqrt[]{13})](/latexrender/pictures/baa85ce3524f819e114b426cf40d0805.png)
, vc multiplicou o 13 pelo 8. e depois dividiu pelo 8 do denominador para chegar no 13 não é ?
-
neoreload
- Usuário Dedicado

-
- Mensagens: 27
- Registrado em: Sáb Ago 09, 2014 16:15
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Simplificação - Ajuda Dúvidas em relação a simplificação
por wgf » Qui Mai 16, 2013 12:56
- 1 Respostas
- 2358 Exibições
- Última mensagem por DanielFerreira

Dom Mai 19, 2013 18:03
Equações
-
- [SIMPLIFICAÇÃO] Simplificação expoentes
por brunnkpol » Ter Mai 07, 2013 17:00
- 1 Respostas
- 1833 Exibições
- Última mensagem por DanielFerreira

Sex Mai 10, 2013 00:40
Aritmética
-
- a sua resposta!!
por weverton » Seg Jul 12, 2010 18:44
- 1 Respostas
- 1379 Exibições
- Última mensagem por weverton

Seg Jul 12, 2010 19:22
Progressões
-
- Nao comsegui axa a resposta ...
por jean » Sáb Nov 29, 2008 17:44
- 2 Respostas
- 2034 Exibições
- Última mensagem por jean

Sáb Nov 29, 2008 21:45
Pedidos
-
- Discordância de resposta
por timoteo » Qua Abr 10, 2013 13:02
- 3 Respostas
- 2760 Exibições
- Última mensagem por DanielFerreira

Ter Abr 16, 2013 21:22
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
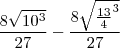
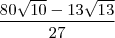

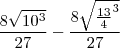
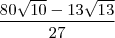


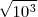 .
.

=
![8/27(10\sqrt[]{10}-13/8\sqrt[]{13}) 8/27(10\sqrt[]{10}-13/8\sqrt[]{13})](/latexrender/pictures/baa85ce3524f819e114b426cf40d0805.png) , vc multiplicou o 13 pelo 8. e depois dividiu pelo 8 do denominador para chegar no 13 não é ?
, vc multiplicou o 13 pelo 8. e depois dividiu pelo 8 do denominador para chegar no 13 não é ?