Se A = {x
 Naturais | x = 4n, com n
Naturais | x = 4n, com n  Naturais}
Naturais}B = {x
 Naturais * |
Naturais * | 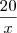 = n, com n
= n, com n  Naturais}
Naturais}então o número de elementos de A
 B é:
B é:a) 3 b) 2 c) 4 d) 6 e) 8
a resposta do gabarito é a letra b.
Já tentei somar as e equações, mas o resultado é n =
![\sqrt[2]{5} \sqrt[2]{5}](/latexrender/pictures/28fccd6e3bab3b28511a875ab32e94c3.png) .
.
 Naturais | x = 4n, com n
Naturais | x = 4n, com n  Naturais}
Naturais} Naturais * |
Naturais * | 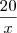 = n, com n
= n, com n  Naturais}
Naturais} B é:
B é:![\sqrt[2]{5} \sqrt[2]{5}](/latexrender/pictures/28fccd6e3bab3b28511a875ab32e94c3.png) .
.





Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

