pelos pontos (0,5) e (10,0) e o ponto (a,b) pertencente a essa reta, conforme mostra a figura
abaixo

Sabendo-se que a área do triângulo de vértices nos pontos (0,5), (0,b) e (a,b) é igual a 4 unidades
de área, calcule, em unidades de área, a área do retângulo sombreado.
Já fiz várias equações e não consegui chegar a área da região sombreada.


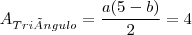 , teremos que
, teremos que 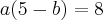
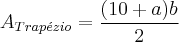
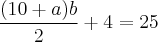

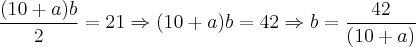
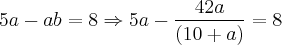

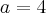 na área do triângulo dado:
na área do triângulo dado: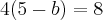
 , como a área do retângulo e dado por
, como a área do retângulo e dado por 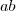 , logo a área do retãngulo sombreado é
, logo a área do retãngulo sombreado é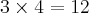 unidades de área.
unidades de área.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)