 por dandara » Seg Dez 29, 2014 10:07
por dandara » Seg Dez 29, 2014 10:07
A reta r tem equação x+3y-6=0. Qual é a área da região determinada pela intersecção da reta r com os eixos coordenados?
-
dandara
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Ter Set 23, 2014 14:37
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por nakagumahissao » Seg Dez 29, 2014 14:05
por nakagumahissao » Seg Dez 29, 2014 14:05
Para encontrarmos os pontos de interseção, deveremos encontrar (0,y) e (x, 0) usando a equação da reta dada:
x + 3y - 6 = 0
Fazendo x = 0, temos que:
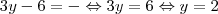
Assim, (0,2) é um dos pontos de interseção com o eixo y.
O outro ponto será:
Fazendo y = 0:
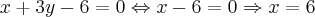
O ponto será (6, 0)
Temos agora um triângulo retângulo onde a base mede 6, a altura mede 2. Assim, a área deverá ser:
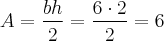
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equação da Reta] Reta que passa por pontos do plano.
por acorreia » Qua Mai 02, 2012 17:31
- 1 Respostas
- 2472 Exibições
- Última mensagem por Russman

Qua Mai 02, 2012 21:25
Geometria Analítica
-
- [Estudo da reta] Determinar a equação de uma reta
por Isabelagarcia » Qui Jul 24, 2014 23:45
- 0 Respostas
- 1600 Exibições
- Última mensagem por Isabelagarcia

Qui Jul 24, 2014 23:45
Geometria Analítica
-
- [Equação da reta] Encontrando equação paramétrica.
por Vitor Sanches » Qua Jun 26, 2013 17:54
- 0 Respostas
- 6098 Exibições
- Última mensagem por Vitor Sanches

Qua Jun 26, 2013 17:54
Geometria Analítica
-
- Equação da Reta
por aline2010 » Dom Jun 13, 2010 23:16
- 1 Respostas
- 1661 Exibições
- Última mensagem por Elcioschin

Seg Jun 14, 2010 12:16
Geometria Analítica
-
- Equação da reta
por marcio277 » Sex Nov 19, 2010 15:04
- 1 Respostas
- 1530 Exibições
- Última mensagem por Molina

Sex Nov 19, 2010 15:13
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



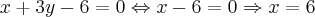
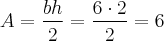



 , avisa que eu resolvo.
, avisa que eu resolvo.

