 por Fernandobertolaccini » Qui Dez 25, 2014 18:16
por Fernandobertolaccini » Qui Dez 25, 2014 18:16
Duas resistências elétricas R1 e R2 estão ligadas em paralelo, ou seja, a resistência equivalente R é dada por
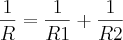
Supondo que R1= 30 ohms e R2 = 50 ohms , calcule a variação de R se:
a) R1 aumenta de 0,03 ohms e R2 diminui de 0,05 ohms
b) R1 diminui de 0,07 ohms e R2 aumenta de 0,04 ohms .
Resp: a) dR = 0,0047 ohms
b) dR = -0,022 ohms
Como chego neste resultado?
Obrigado !
-
Fernandobertolaccini
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Qui Mai 01, 2014 10:27
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Licenciatura em Física
- Andamento: cursando
 por adauto martins » Sex Dez 26, 2014 12:00
por adauto martins » Sex Dez 26, 2014 12:00

...
a)

b)analogo a a)
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por Russman » Sáb Dez 27, 2014 00:21
por Russman » Sáb Dez 27, 2014 00:21
De fato, dada uma função

,

.
Daí, como a função "resistência equivalente"
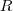
é função das duas resistências
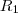
e
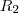
, então

.
Calculando as derivadas parciais você concluirá que, após aplicar a derivação da função composta e , em seguida, da cadeia,


e, portanto,

A resistência equivalente é 18,75.
Na letra a) tome

e

. Analogamente na letra b).
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Aplicação da diferencial com varias variáveis
por Fernandobertolaccini » Ter Dez 23, 2014 19:19
- 1 Respostas
- 2440 Exibições
- Última mensagem por adauto martins

Qua Dez 24, 2014 17:45
Cálculo: Limites, Derivadas e Integrais
-
- Função de várias variaveis e series
 por leticiapires52 » Seg Abr 25, 2016 13:56
por leticiapires52 » Seg Abr 25, 2016 13:56
- 2 Respostas
- 2069 Exibições
- Última mensagem por adauto martins

Seg Mai 02, 2016 14:53
Funções
-
- [Limite]Limite de uma funçao de varias variaveis
por TheKyabu » Seg Fev 04, 2013 22:01
- 3 Respostas
- 3474 Exibições
- Última mensagem por young_jedi

Ter Fev 05, 2013 19:47
Cálculo: Limites, Derivadas e Integrais
-
- Derivada com várias variáveis
por kryzay » Seg Mai 14, 2012 09:23
- 2 Respostas
- 2679 Exibições
- Última mensagem por kryzay

Seg Mai 14, 2012 10:58
Cálculo: Limites, Derivadas e Integrais
-
- Limite de várias variáveis
por braddock » Seg Mai 05, 2014 04:06
- 2 Respostas
- 5039 Exibições
- Última mensagem por braddock

Seg Mai 05, 2014 22:17
Cálculo
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
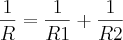 Supondo que R1= 30 ohms e R2 = 50 ohms , calcule a variação de R se:
Supondo que R1= 30 ohms e R2 = 50 ohms , calcule a variação de R se:

 ...
...
 ,
,  .
.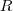 é função das duas resistências
é função das duas resistências 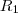 e
e 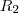 , então
, então .
.


 e
e  . Analogamente na letra b).
. Analogamente na letra b).