 por fasaatyro » Seg Dez 01, 2014 21:56
por fasaatyro » Seg Dez 01, 2014 21:56
![\int\frac{(1+\sqrt[]{x}³}{\sqrt[]{x}}dx \int\frac{(1+\sqrt[]{x}³}{\sqrt[]{x}}dx](/latexrender/pictures/a6ec631f77cc362a753bf7e7aeb23e55.png)
por favor encontrei como resultado
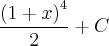
está correto????
-
fasaatyro
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Seg Dez 01, 2014 21:41
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura matematica
- Andamento: cursando
 por adauto martins » Ter Dez 02, 2014 16:37
por adauto martins » Ter Dez 02, 2014 16:37
seria essa I=
![\int_{}^{}({1+\sqrt[]{x}})^{3}dx/(\sqrt[]{x}) \int_{}^{}({1+\sqrt[]{x}})^{3}dx/(\sqrt[]{x})](/latexrender/pictures/cad4774f7b49c8fae7611b8e6646a084.png)
,se nao for,vamos nessa mesmo...
faz-se
![u=1+\sqrt[]{x}\Rightarrow du=(1/2).(1/\sqrt[]{x})dx u=1+\sqrt[]{x}\Rightarrow du=(1/2).(1/\sqrt[]{x})dx](/latexrender/pictures/177c95970becea14daa63e93cea0fba1.png)
,logo
![I=2.(\int_{}^{}{u}^{3}du)=2.{u}^{3+1}/(3+1)+c=(1/2)({1+\sqrt[]{x}})^{4}+c I=2.(\int_{}^{}{u}^{3}du)=2.{u}^{3+1}/(3+1)+c=(1/2)({1+\sqrt[]{x}})^{4}+c](/latexrender/pictures/448a13f5d8e9b626c609266dda2b22ab.png)
...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral indefinida
por gdarius » Ter Mar 16, 2010 15:57
- 5 Respostas
- 5637 Exibições
- Última mensagem por DanielFerreira

Sáb Mar 31, 2012 19:32
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinida
 por CrazzyVi » Ter Ago 17, 2010 21:41
por CrazzyVi » Ter Ago 17, 2010 21:41
- 1 Respostas
- 2715 Exibições
- Última mensagem por Lucio Carvalho

Qua Ago 18, 2010 08:27
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinida
por felipealves » Ter Jun 21, 2011 11:48
- 3 Respostas
- 3993 Exibições
- Última mensagem por felipealves

Ter Jun 21, 2011 20:59
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] indefinida
por Aliocha Karamazov » Qui Mar 01, 2012 20:30
- 7 Respostas
- 5057 Exibições
- Última mensagem por Aliocha Karamazov

Sáb Mar 03, 2012 21:59
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinida - 2
por DanielFerreira » Sáb Mar 31, 2012 18:31
- 1 Respostas
- 2073 Exibições
- Última mensagem por LuizAquino

Sáb Mar 31, 2012 18:53
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int\frac{(1+\sqrt[]{x}³}{\sqrt[]{x}}dx \int\frac{(1+\sqrt[]{x}³}{\sqrt[]{x}}dx](/latexrender/pictures/a6ec631f77cc362a753bf7e7aeb23e55.png) por favor encontrei como resultado
por favor encontrei como resultado 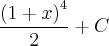 está correto????
está correto????
![\int\frac{(1+\sqrt[]{x}³}{\sqrt[]{x}}dx \int\frac{(1+\sqrt[]{x}³}{\sqrt[]{x}}dx](/latexrender/pictures/a6ec631f77cc362a753bf7e7aeb23e55.png) por favor encontrei como resultado
por favor encontrei como resultado 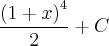 está correto????
está correto????
![\int_{}^{}({1+\sqrt[]{x}})^{3}dx/(\sqrt[]{x}) \int_{}^{}({1+\sqrt[]{x}})^{3}dx/(\sqrt[]{x})](/latexrender/pictures/cad4774f7b49c8fae7611b8e6646a084.png) ,se nao for,vamos nessa mesmo...
,se nao for,vamos nessa mesmo...![u=1+\sqrt[]{x}\Rightarrow du=(1/2).(1/\sqrt[]{x})dx u=1+\sqrt[]{x}\Rightarrow du=(1/2).(1/\sqrt[]{x})dx](/latexrender/pictures/177c95970becea14daa63e93cea0fba1.png) ,logo
,logo ![I=2.(\int_{}^{}{u}^{3}du)=2.{u}^{3+1}/(3+1)+c=(1/2)({1+\sqrt[]{x}})^{4}+c I=2.(\int_{}^{}{u}^{3}du)=2.{u}^{3+1}/(3+1)+c=(1/2)({1+\sqrt[]{x}})^{4}+c](/latexrender/pictures/448a13f5d8e9b626c609266dda2b22ab.png) ...
...