Seja T: R²----->R³ uma transformação linear com a matriz:
T = 1 -1
0 1
-2 3
Para que B={e1,e2}, base canonica do R², e B'={ (1,0,1) , (-2,0,1) , (0,1,0)} base do R³. Qual a imagem do vetor (2,-3) pela T.
obrigado.
por rodrigojuara » Dom Nov 30, 2014 15:05
por adauto martins » Seg Dez 01, 2014 16:12
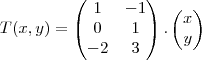
,pela transf.T(x,y) sob a matriz dada...aqui vc nao especificou a base a ser calculada,vou calcular segundo a transformaçao aplicada na matriz em questao e na base referente a matriz q. eh B...entao
Usuários navegando neste fórum: Nenhum usuário registrado e 20 visitantes
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
o ângulo entre o eixo horizontal e o afixo 
. O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
o ângulo complementar. Então 
. Como 
, o ângulo que o afixo 
formará com a horizontal será , mas negativo pois tem de ser no quarto quadrante. Se 
, então 
. Como módulo é um: 
.
.