Bom, sou novo aqui no fórum e já começo com uma dúvida, sinto por imcomodar-vos.
Pois bem:
A questão pede para eu dizer se o vetor abaixo pertence a W = [(2,1,0,3), (3,-1,5,2), (-1,0,2,1)]
O vetor é v = (2,3,-7,3)
Eu fiz a relaçao v = aW1+bW2+W3 (onde Wn são os vetores de W, enfim, fiz a relação de combinação linear)
Dai obtive a matriz ampliada que escalonei e me deu a seguinte situação:
1 0 0 -12/5
0 1 0 -1
0 0 1 -1
0 0 0 0
Ai entra a dúvida:
Substituindo o que encontrei em a,b e c não dá o vetor v! Mas como isso se isso foi exatamente o que a matriz me desvendou?
Ou eu fiz tudo errado... Ou eu fiz tudo errado rs
Então agradeceria muito quem me ajudasse nessa questão.
Ps: Estou usando o fórum no celular, por curiosidade, é possível usar o sistema Latex para colocar as fórmulas bonitinhas pelo celular? Ou só na versão desktop?
Abs.


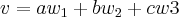 ...
...![(2,3,-7,3)=a(2,1,0,3)+b(3,-1,5,2)+c(-1,0,2,1)...[tex]\Rightarrow 2a+3b-c=2,a-b=3,5b+2c=-7,3a+2b+c=3... (2,3,-7,3)=a(2,1,0,3)+b(3,-1,5,2)+c(-1,0,2,1)...[tex]\Rightarrow 2a+3b-c=2,a-b=3,5b+2c=-7,3a+2b+c=3...](/latexrender/pictures/94a2085d4d392bfa25ac50f419bc620b.png) sao as equaçoes,colocando-as em uma matriz completa ...
sao as equaçoes,colocando-as em uma matriz completa ... ,escalonandom,teremos
,escalonandom,teremos

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)