 por Pessoa Estranha » Sáb Nov 22, 2014 14:47
por Pessoa Estranha » Sáb Nov 22, 2014 14:47
Olá!
Preciso de ajuda para a seguinte questão: "Verifique se existem homomorfismos não nulo de (a)
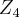
em

."
Por favor, preciso muito de ajuda. Não sei nem por onde começar!
Muito Obrigada!
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por adauto martins » Dom Nov 23, 2014 12:35
por adauto martins » Dom Nov 23, 2014 12:35
dados
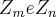
tais q. o mdc(m,n)=1,ou seja primos entre si ,o unico homomorfismo ente esses grupos e o homomorfismo identicamente nulo...logo nao ha homomorfismo identicamente nao nulos entre
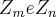
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por Pessoa Estranha » Dom Nov 23, 2014 13:07
por Pessoa Estranha » Dom Nov 23, 2014 13:07
Agradeço muito a sua ajuda!
Só uma pergunta: isso vem por um resultado (teorema, proposição) ?
Qual o livro que você utiliza ou utilizou para estudar esses assuntos?
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por adauto martins » Dom Nov 23, 2014 13:17
por adauto martins » Dom Nov 23, 2014 13:17
isso vem como consequencia direta de subgrupos e grupos geradores...o livro base:introduçao a algebra-adilson gonçalves-edicoes do impa...e muita coisa na net mesmo
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por Pessoa Estranha » Dom Nov 23, 2014 14:26
por Pessoa Estranha » Dom Nov 23, 2014 14:26
Bom, então quer dizer que de Z4 em Z8 e de Z8 em Z4, como 4 e 8 não são primos entre si, há homomorfismos não nulos?
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por adauto martins » Dom Nov 23, 2014 19:53
por adauto martins » Dom Nov 23, 2014 19:53
seja
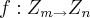
tal q. f e um homomorfismo injetivo,e nucl(f)={e},onde nuc(f) e o nucleo da aplicaçao,entao diz-se q. f e um homomorfismo identicamente nulo de
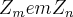
...entao pela colocaçao acima resolva e tire suas duvidas, e resolva o exercicio:
se mdc(m,n)=1,entao
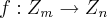
e um homomorfismo identicamente nulo,caso contrario homomorfismo identicamente nao nulo...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Estruturas Algébricas] Homomorfismo
por Pessoa Estranha » Qui Nov 13, 2014 22:31
- 4 Respostas
- 2244 Exibições
- Última mensagem por adauto martins

Sex Nov 21, 2014 16:58
Álgebra Elementar
-
- Estruturas algébricas
por Eliane Maria » Qua Abr 25, 2012 01:01
- 12 Respostas
- 9192 Exibições
- Última mensagem por fraol

Ter Mai 01, 2012 23:42
Álgebra Elementar
-
- Anéis ( Estruturas algébricas)
por Crist » Qui Mar 20, 2014 15:32
- 1 Respostas
- 2899 Exibições
- Última mensagem por adauto martins

Seg Mar 14, 2016 19:47
Teoria dos Números
-
- [Estruturas algébricas] Anéis
por Crist » Sáb Mar 22, 2014 16:45
- 1 Respostas
- 2091 Exibições
- Última mensagem por adauto martins

Ter Jan 13, 2015 15:45
Álgebra Elementar
-
- [Estruturas Algébricas] Relações
por Pessoa Estranha » Ter Abr 29, 2014 18:28
- 1 Respostas
- 1800 Exibições
- Última mensagem por adauto martins

Sex Dez 05, 2014 17:53
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
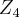 em
em  ."
."
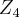 em
em  ."
."
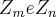 tais q. o mdc(m,n)=1,ou seja primos entre si ,o unico homomorfismo ente esses grupos e o homomorfismo identicamente nulo...logo nao ha homomorfismo identicamente nao nulos entre
tais q. o mdc(m,n)=1,ou seja primos entre si ,o unico homomorfismo ente esses grupos e o homomorfismo identicamente nulo...logo nao ha homomorfismo identicamente nao nulos entre 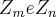




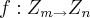 tal q. f e um homomorfismo injetivo,e nucl(f)={e},onde nuc(f) e o nucleo da aplicaçao,entao diz-se q. f e um homomorfismo identicamente nulo de
tal q. f e um homomorfismo injetivo,e nucl(f)={e},onde nuc(f) e o nucleo da aplicaçao,entao diz-se q. f e um homomorfismo identicamente nulo de 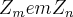 ...entao pela colocaçao acima resolva e tire suas duvidas, e resolva o exercicio:
...entao pela colocaçao acima resolva e tire suas duvidas, e resolva o exercicio: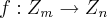 e um homomorfismo identicamente nulo,caso contrario homomorfismo identicamente nao nulo...
e um homomorfismo identicamente nulo,caso contrario homomorfismo identicamente nao nulo...