Suponhamos que no instante t(minutos), a pressão seja dada por P(t) = 20 + 2t, com
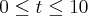. Se em t=0 o volume é de 60cm³, determine a taxa de variação do volume por unidade de variação do tempo quando T=5. Valeew !!
por Fernandobertolaccini » Sáb Out 25, 2014 09:57
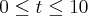. Se em t=0 o volume é de 60cm³, determine a taxa de variação do volume por unidade de variação do tempo quando T=5. 
por adauto martins » Sáb Out 25, 2014 11:42
por Fernandobertolaccini » Sáb Out 25, 2014 11:57
por Fernandobertolaccini » Sáb Out 25, 2014 12:12
adauto martins escreveu:taxa de variaçao de uma quantidade e dada pela derivada dessa quantidade em funçao do parametro a qual depende a quantidade,no caso V=V(t)...entao:dV/dt...pela equaçao de P=P(t),teremos:P=k/V...k/V(t)=20+2t...V(t)=k/(20+2t)...
dV/dt=2.k.ln(20+2t)...t=0,tem-se 60=2kln(20)...aqui acha-se k e depois,calcula-se V,para T=5...
por adauto martins » Sáb Out 25, 2014 12:21
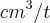,t(unidade de tempo)por Fernandobertolaccini » Sáb Out 25, 2014 12:45
adauto martins escreveu:dV/dt=2(30/ln(20)).ln(20+2t)=60.ln(20+2t-20)=60.ln(2t)...p/t=5,teriamos:
dV/dt=60.ln(10)=60.(2,3)=138
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)