 por starlord » Sáb Ago 23, 2014 19:30
por starlord » Sáb Ago 23, 2014 19:30
Olá, queria ajuda pra calcular esse limite cabeludo que veio na minha primeira lista de cálculo hehe em anexo a foto do limite.
- Anexos
-
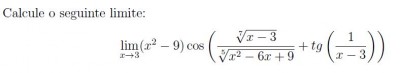
-
starlord
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Ago 23, 2014 19:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Computação
- Andamento: cursando
 por adauto martins » Qui Out 23, 2014 18:07
por adauto martins » Qui Out 23, 2014 18:07
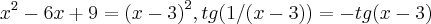
,pois tg1
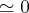
...logo:
L=
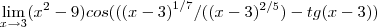
L=
![\lim_{x\rightarrow3}(x+3)(x-3)cos((\sqrt[7]{x-3})/(\sqrt[5]({{x-3})^{2}})-tg(x-3)) \lim_{x\rightarrow3}(x+3)(x-3)cos((\sqrt[7]{x-3})/(\sqrt[5]({{x-3})^{2}})-tg(x-3))](/latexrender/pictures/cd6eafe84e0bd119967cc307f762eb68.png)
,
(
![cos((\sqrt[7]{x-3})/(\sqrt[5]({{x-3})^{2}})-tg(x-3)) cos((\sqrt[7]{x-3})/(\sqrt[5]({{x-3})^{2}})-tg(x-3))](/latexrender/pictures/8a86d13e6316a611b013a5ad9b310388.png)
)
^{11}})-tg(x-3)) cos((1/(\sqrt[35]({{x-3})^{11}})-tg(x-3))](/latexrender/pictures/c0a92cbba0a317a9bde1200df47b1044.png)
...
o argumento do cosx,e um termo muito grande q. tende ao infinito,logo o maior valor q. o cosx pode assumir e 1,entao:
L=
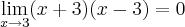
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Qui Out 23, 2014 23:11
por adauto martins » Qui Out 23, 2014 23:11
eita,mais uma correçao...
o argumento de cosx se torna infinito,devido ao radical (
![R=1/(\sqrt[35]{({x-3})^{11}} R=1/(\sqrt[35]{({x-3})^{11}}](/latexrender/pictures/56f1a221454d0dcc7891148428236cf8.png)
),logo cos(R-tg(x-3))=0...
fato esse q. se pode calcular fazendo cos(R+tg(x-3))...obrigado
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limites] Como calcular este limite?
por alienpuke » Qui Out 01, 2015 11:18
- 1 Respostas
- 1938 Exibições
- Última mensagem por nakagumahissao

Qui Out 01, 2015 23:59
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Como calcular este limite?
por alienpuke » Qua Set 30, 2015 23:32
- 1 Respostas
- 1983 Exibições
- Última mensagem por nakagumahissao

Sex Out 02, 2015 00:05
Cálculo: Limites, Derivadas e Integrais
-
- [Limites]Como calcular esse limite trigonometrico?
por IlgssonBraga » Dom Mar 02, 2014 14:59
- 2 Respostas
- 1995 Exibições
- Última mensagem por IlgssonBraga

Dom Mar 02, 2014 17:01
Cálculo: Limites, Derivadas e Integrais
-
- [Limites]Preciso de ajuda para calcular alguns limites
por Pessoa Estranha » Ter Jul 16, 2013 17:15
- 2 Respostas
- 4759 Exibições
- Última mensagem por LuizAquino

Qua Jul 17, 2013 09:12
Cálculo: Limites, Derivadas e Integrais
-
- Como achar esse valor seno?
por angsrom » Qua Ago 03, 2011 09:21
- 2 Respostas
- 1993 Exibições
- Última mensagem por supertag

Qui Ago 04, 2011 01:18
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



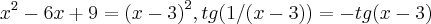 ,pois tg1
,pois tg1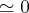 ...logo:
...logo: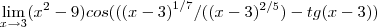
![\lim_{x\rightarrow3}(x+3)(x-3)cos((\sqrt[7]{x-3})/(\sqrt[5]({{x-3})^{2}})-tg(x-3)) \lim_{x\rightarrow3}(x+3)(x-3)cos((\sqrt[7]{x-3})/(\sqrt[5]({{x-3})^{2}})-tg(x-3))](/latexrender/pictures/cd6eafe84e0bd119967cc307f762eb68.png) ,
,![cos((\sqrt[7]{x-3})/(\sqrt[5]({{x-3})^{2}})-tg(x-3)) cos((\sqrt[7]{x-3})/(\sqrt[5]({{x-3})^{2}})-tg(x-3))](/latexrender/pictures/8a86d13e6316a611b013a5ad9b310388.png) )
)^{11}})-tg(x-3)) cos((1/(\sqrt[35]({{x-3})^{11}})-tg(x-3))](/latexrender/pictures/c0a92cbba0a317a9bde1200df47b1044.png) ...
...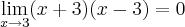

![R=1/(\sqrt[35]{({x-3})^{11}} R=1/(\sqrt[35]{({x-3})^{11}}](/latexrender/pictures/56f1a221454d0dcc7891148428236cf8.png) ),logo cos(R-tg(x-3))=0...
),logo cos(R-tg(x-3))=0...

 .
.



