 M(2,2)/ b = a d = -a
M(2,2)/ b = a d = -aEntão pensei; fácil, basta provar que as propriedades de soma de 2 matrizes estão contidas no subespaço assim como o produto de 2 matrizes igual ao produto do mesmo quando sua ordem for trocada...
-Para a soma, Ok.
-Mas para o produto, nem
Queria ajuda de vocês para ver se estou certo nisto ou o gabarito está correto. Ele afirma ser verdade que W é subspaço de M.
Mas olhem comigo isto:
Se
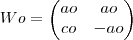 e
e 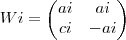
Então
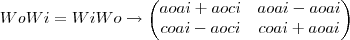 =
= 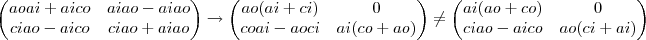
Poderiam me dar uma luz, galera?


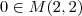 :
: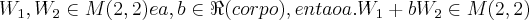 ,aqui multiplicaçao por escalar e nao multiplicaçao de matruizes,como vc fez,entao:
,aqui multiplicaçao por escalar e nao multiplicaçao de matruizes,como vc fez,entao: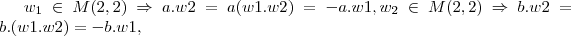 ,LOGO:
,LOGO: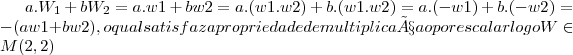

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)