Simplesmente não consigo resolver exercícios que propõem que se ache o resultado de uma determinada operação a partir do resultado de outra.
Por exemplo:
Sabendo que
cossec x/sec x + sec x/cossec x = 5, o valor de
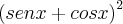 é:
é:Ou então:
Se tg x + cotg x = 3, calcule sen 2x.
Estou com todas as identidades (cossec x = 1/sen x; etc.) em mente, bem como as fórmulas derivadas da Relação Fundamental, e também mantendo em mente que
sen 2x = 2senx.cosx, e cos 2x =
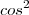 -
- 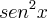 , e as outras que se derivam a partir daí, bem como as da tangente.
, e as outras que se derivam a partir daí, bem como as da tangente. Mas obviamente há alguma relação que não consigo enxergar. Qualquer ajuda será muito bem-vinda.
Obrigado pela atenção.


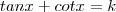 . Se você fizer k = 5 e depois igual 3 você terá exatamente as duas equações que expôs (certifique-se que o primeiro membro da 1ª eq. é o mesmo que o escrever tan x + cot x .) .
. Se você fizer k = 5 e depois igual 3 você terá exatamente as duas equações que expôs (certifique-se que o primeiro membro da 1ª eq. é o mesmo que o escrever tan x + cot x .) . 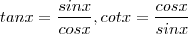 .
. 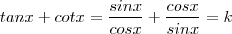 . Ou ainda ,
. Ou ainda , 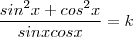 .Mas
.Mas 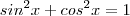 e também que
e também que 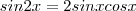 . Assim ,
. Assim , 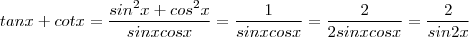 o que implica
o que implica 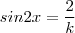 . Segue daí que podemos escolher qualquer k maior ou igual a 2 em módulo (pois seno é limitado por 1) .
. Segue daí que podemos escolher qualquer k maior ou igual a 2 em módulo (pois seno é limitado por 1) .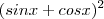 note que
note que 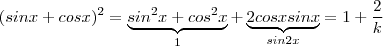




 .
.



