


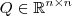 (espaço das matrizes n por n sobre R) com tal propriedade
(espaço das matrizes n por n sobre R) com tal propriedade 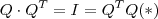 .Como de costume as entradas de uma matriz A é representado por
.Como de costume as entradas de uma matriz A é representado por 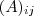 ou simplesmente
ou simplesmente 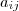 ,com esta notação e da definição de produto de matrizes , temos
,com esta notação e da definição de produto de matrizes , temos 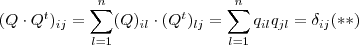 (Delta de Kronecker) .
(Delta de Kronecker) . 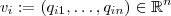 .Aplicando o produto interno (usual do R^n) em quaisquer pares de vetores (v_i,v_j) obteremos exatamente a soma em (**) . Segue daí que os n vetores v_i são ortogonais e unitários . Ou seja , as linhas da matrizes Q são vetores ortonormais .Analogamente mostra-se que as colunas de Q são vetores ortonormais e daí o nome matriz ortogonal .
.Aplicando o produto interno (usual do R^n) em quaisquer pares de vetores (v_i,v_j) obteremos exatamente a soma em (**) . Segue daí que os n vetores v_i são ortogonais e unitários . Ou seja , as linhas da matrizes Q são vetores ortonormais .Analogamente mostra-se que as colunas de Q são vetores ortonormais e daí o nome matriz ortogonal .

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 .
.
 :
: