Festival de cinema.

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

Festival de cinema.

Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
Responder

Festival de cinema.

Mensagempor magaleao » Qui Dez 31, 2009 11:16

Olá, estou precisando de ajuda..............

Em um festival de cinema, sete filmes diferentes, entre eles apenas duas comédias, serão exibidos, um a cada dia e no mesmo horário, durante uma semana. Para anunciar esses filmes será confeccionado um cartaz com o título de cada filme e o dia de sua exibição. A quantidade máxima de maneiras distintas de apresentação dos filmes, de modo que as comédias não sejam exibidas em dias consecutivos, corresponde a:


Desde já agradeço...
magaleao
Usuário Ativo
Usuário Ativo
 
Mensagens: 10
Registrado em: Qui Dez 17, 2009 13:33
Formação Escolar: GRADUAÇÃO
Andamento: formado
Voltar ao topo

Re: Festival de cinema.

Mensagempor MarceloFantini » Qui Dez 31, 2009 16:45

Boa tarde Maga!

O número total de possibilidades para assistir aos filmes é 7!.

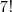
O número de jeitos de exibir os filmes, sendo que as comédias são mostradas CONSECUTIVAMENTE é 6!\times2!.

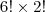
Portanto, o número de jeitos distintos de exibir os filmes sendo que as comédias não são consecutivas é 7! - 6!\times2! = 3600.

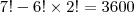
Um abraço e Feliz Ano Novo!
Futuro MATEMÁTICO
e^{\pi \cdot i} +1 = 0
MarceloFantini
Colaborador Moderador
Colaborador Moderador
 
Mensagens: 3126
Registrado em: Seg Dez 14, 2009 11:41
Formação Escolar: GRADUAÇÃO
Andamento: formado
Voltar ao topo
Responder

Voltar para Desafios Médios

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 


Tópico Popular

Assunto: cálculo de limites
Autor: Hansegon - Seg Ago 25, 2008 11:29

Bom dia.

Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado

\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]

Assunto: cálculo de limites
Autor: Molina - Seg Ago 25, 2008 13:25

\lim_{x\rightarrow-1} \frac{{x}^{3}+1}{{x}^{2}-1}

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.

Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo. :y:

Caso ainda não tenha dado uma :idea:, avisa que eu resolvo.

Bom estudo!

Assunto: cálculo de limites
Autor: Guill - Dom Abr 08, 2012 16:03

\lim_{x\rightarrow-1}\frac{x^3+1}{x^2-1}

\lim_{x\rightarrow-1}\frac{(x+1)(x^2-x+1)}{(x+1)(x-1)}

\lim_{x\rightarrow-1}\frac{(x^2-x+1)}{(x-1)}=\frac{-3}{2}

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

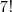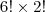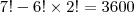Índice do fórum