 por YuriFreire » Ter Ago 19, 2014 23:27
por YuriFreire » Ter Ago 19, 2014 23:27
Boa noite,
Gostaria de compreender a seguinte questão em anexo.
Como posso encontrar a equação para uma reta vertical que passa pelo ponto y = 4/3 se uma reta vertical não tem como achar coeficiente angular? Essa reta sendo vertical com x = -1 não é a equação x = -1? Ou seja para todo y, x = -1.
- Anexos
-

-
YuriFreire
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sex Ago 08, 2014 00:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Medicina/Licenciatura em Matemática
- Andamento: cursando
 por YuriFreire » Sáb Ago 23, 2014 22:07
por YuriFreire » Sáb Ago 23, 2014 22:07
Alguém??
Ainda to precisando de ajuda. Sei que é questão besta.
Grato,
Yuri Freire
-
YuriFreire
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sex Ago 08, 2014 00:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Medicina/Licenciatura em Matemática
- Andamento: cursando
 por DanielFerreira » Sáb Ago 23, 2014 22:25
por DanielFerreira » Sáb Ago 23, 2014 22:25
Olá
Yuri,
boa noite!
A equação da reta é dada por
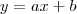
. Ora, marquemos o ponto (- 1, 4/3) no plano cartesiana e prolonguemos a vertical; como podes notar, a equação da reta também passará pelo ponto (- 1, 0).
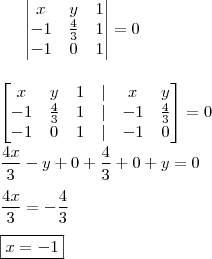
Resta-nos encontrar a equação...
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por YuriFreire » Seg Set 01, 2014 22:42
por YuriFreire » Seg Set 01, 2014 22:42
Obrigado meu caro!
Aprendi a fazer!!
-
YuriFreire
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sex Ago 08, 2014 00:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Medicina/Licenciatura em Matemática
- Andamento: cursando
 por DanielFerreira » Dom Set 07, 2014 21:23
por DanielFerreira » Dom Set 07, 2014 21:23
Que bom! Até a próxima.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equação da Reta] Reta que passa por pontos do plano.
por acorreia » Qua Mai 02, 2012 17:31
- 1 Respostas
- 2475 Exibições
- Última mensagem por Russman

Qua Mai 02, 2012 21:25
Geometria Analítica
-
- [Estudo da reta] Determinar a equação de uma reta
por Isabelagarcia » Qui Jul 24, 2014 23:45
- 0 Respostas
- 1601 Exibições
- Última mensagem por Isabelagarcia

Qui Jul 24, 2014 23:45
Geometria Analítica
-
- [Equação da reta] Encontrando equação paramétrica.
por Vitor Sanches » Qua Jun 26, 2013 17:54
- 0 Respostas
- 6098 Exibições
- Última mensagem por Vitor Sanches

Qua Jun 26, 2013 17:54
Geometria Analítica
-
- Equação da Reta
por aline2010 » Dom Jun 13, 2010 23:16
- 1 Respostas
- 1662 Exibições
- Última mensagem por Elcioschin

Seg Jun 14, 2010 12:16
Geometria Analítica
-
- Equação da reta
por marcio277 » Sex Nov 19, 2010 15:04
- 1 Respostas
- 1530 Exibições
- Última mensagem por Molina

Sex Nov 19, 2010 15:13
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


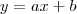 . Ora, marquemos o ponto (- 1, 4/3) no plano cartesiana e prolonguemos a vertical; como podes notar, a equação da reta também passará pelo ponto (- 1, 0).
. Ora, marquemos o ponto (- 1, 4/3) no plano cartesiana e prolonguemos a vertical; como podes notar, a equação da reta também passará pelo ponto (- 1, 0).
