 por Fernandobertolaccini » Sáb Jul 26, 2014 12:24
por Fernandobertolaccini » Sáb Jul 26, 2014 12:24
Sabe-se que o gráfico da função F(x) = raiz cúbica de
![\sqrt[3]{6x^2-x^3} \sqrt[3]{6x^2-x^3}](/latexrender/pictures/49c36bfe7d0a2491bf622096f5f68081.png)
possui uma assintota oblíqua. Determine a equação dessa assintota e prove que a curva de F(x) intercepta a mesma.
resp: y= - x + 2
Muito obrigado ;D
-
Fernandobertolaccini
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Qui Mai 01, 2014 10:27
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Licenciatura em Física
- Andamento: cursando
 por ant_dii » Dom Jul 27, 2014 05:04
por ant_dii » Dom Jul 27, 2014 05:04
Fernandobertolaccini escreveu:Sabe-se que o gráfico da função
F(x) = raiz cúbica de ![\sqrt[3]{6x^2-x^3} \sqrt[3]{6x^2-x^3}](/latexrender/pictures/49c36bfe7d0a2491bf622096f5f68081.png)
possui uma assintota oblíqua. Determine a equação dessa assintota e prove que a curva de F(x) intercepta a mesma.
resp: y= - x + 2
Muito obrigado ;D
Não ficou claro se você quer encontrar a assíntota de
![F(x)=\sqrt[3]{6x^2-x^3} F(x)=\sqrt[3]{6x^2-x^3}](/latexrender/pictures/4da55a84cfa50c7848e175a63871eeee.png)
ou de
![F(x)=\sqrt[3]{\sqrt[3]{6x^2-x^3}} F(x)=\sqrt[3]{\sqrt[3]{6x^2-x^3}}](/latexrender/pictures/09d1ede9bc8a97fe1b791598be9cb1e3.png)
.
Se for o primeiro (ou também o segundo, pois o método é o mesmo) você deve encontrar uma reta que tem equação

tal que
![a=\lim_{x\rightarrow \infty} \left[\frac{F(x)}{x}\right] a=\lim_{x\rightarrow \infty} \left[\frac{F(x)}{x}\right]](/latexrender/pictures/8114f1619925b2ea06816fe89aa9b0dd.png)
ou
![a=\lim_{x\rightarrow -\infty} \left[\frac{F(x)}{x}\right] a=\lim_{x\rightarrow -\infty} \left[\frac{F(x)}{x}\right]](/latexrender/pictures/7758e468413fda650c3b4d6539e3e6b6.png)
e
![b=\lim_{x\rightarrow \infty} \left[F(x)-ax\right] b=\lim_{x\rightarrow \infty} \left[F(x)-ax\right]](/latexrender/pictures/14daeaba209f3d3dcbb1f37b49e0e9d0.png)
ou
![b=\lim_{x\rightarrow \infty} \left[F(x)-ax\right] b=\lim_{x\rightarrow \infty} \left[F(x)-ax\right]](/latexrender/pictures/14daeaba209f3d3dcbb1f37b49e0e9d0.png)
.
Assim,
![a=\lim_{x\rightarrow \pm \infty} \left[\frac{\sqrt[3]{6x^2-x^3}}{x}\right]=\lim_{x\rightarrow \pm \infty} \left[\frac{\sqrt[3]{6x^2-x^3}}{\sqrt[3]{x}}\right]=\newline \newline \lim_{x\rightarrow \pm \infty} \left[\sqrt[3]{\frac{6x^2-x^3}{x^3}}\right]=\lim_{x\rightarrow \pm \infty} \left[\sqrt[3]{\frac{6}{x}-1}\right]=-1 a=\lim_{x\rightarrow \pm \infty} \left[\frac{\sqrt[3]{6x^2-x^3}}{x}\right]=\lim_{x\rightarrow \pm \infty} \left[\frac{\sqrt[3]{6x^2-x^3}}{\sqrt[3]{x}}\right]=\newline \newline \lim_{x\rightarrow \pm \infty} \left[\sqrt[3]{\frac{6x^2-x^3}{x^3}}\right]=\lim_{x\rightarrow \pm \infty} \left[\sqrt[3]{\frac{6}{x}-1}\right]=-1](/latexrender/pictures/a50b9f4470ded97fc393230fa23e2434.png)
e
![b=\lim_{x\rightarrow -\infty} \left[F(x)+ax\right]=\lim_{x\rightarrow -\infty} \left[\sqrt[3]{6x^2-x^3}-(-1)x\right]= b=\lim_{x\rightarrow -\infty} \left[F(x)+ax\right]=\lim_{x\rightarrow -\infty} \left[\sqrt[3]{6x^2-x^3}-(-1)x\right]=](/latexrender/pictures/b491848b03c698ceb63c349342b1c6c0.png)
![=\lim_{x\rightarrow -\infty}\frac{\left[\sqrt[3]{6x^2-x^3}+x\right]\left[(\sqrt[3]{6x^2-x^3})^{2}-x\sqrt[3]{6x^2-x^3}+x^{2}\right]}{\left[(\sqrt[3]{6x^2-x^3})^{2}-x\sqrt[3]{6x^2-x^3}+x^{2}\right]}= =\lim_{x\rightarrow -\infty}\frac{\left[\sqrt[3]{6x^2-x^3}+x\right]\left[(\sqrt[3]{6x^2-x^3})^{2}-x\sqrt[3]{6x^2-x^3}+x^{2}\right]}{\left[(\sqrt[3]{6x^2-x^3})^{2}-x\sqrt[3]{6x^2-x^3}+x^{2}\right]}=](/latexrender/pictures/f0d1216cebab945f018f2a439f75cfe9.png)
![=\lim_{x\rightarrow -\infty}\frac{6x^2}{\left[(\sqrt[3]{6x^2-x^3})^{2}-x\sqrt[3]{6x^2-x^3}+x^{2}\right]}=\frac{6}{3}=2 =\lim_{x\rightarrow -\infty}\frac{6x^2}{\left[(\sqrt[3]{6x^2-x^3})^{2}-x\sqrt[3]{6x^2-x^3}+x^{2}\right]}=\frac{6}{3}=2](/latexrender/pictures/85aac2e0f405555188f86dc4319938be.png)
Tente fazer os cálculos sozinho e verifique porque para encontrar o valor de

usei
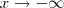
e não
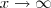
.
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Assintota obliqua de uma função
por Fernandobertolaccini » Seg Ago 18, 2014 18:24
- 0 Respostas
- 2218 Exibições
- Última mensagem por Fernandobertolaccini

Seg Ago 18, 2014 18:24
Cálculo: Limites, Derivadas e Integrais
-
- assintota
por DyegoBrum » Seg Set 19, 2011 13:30
- 2 Respostas
- 2051 Exibições
- Última mensagem por DyegoBrum

Qua Set 21, 2011 15:09
Cálculo: Limites, Derivadas e Integrais
-
- limite {assintota}
por DyegoBrum » Seg Set 19, 2011 13:38
- 1 Respostas
- 1683 Exibições
- Última mensagem por LuizAquino

Seg Set 19, 2011 17:27
Cálculo: Limites, Derivadas e Integrais
-
- assíntota inclinada
por Priscilla Correa » Sex Mai 18, 2012 17:53
- 2 Respostas
- 3345 Exibições
- Última mensagem por Priscilla Correa

Sáb Mai 19, 2012 20:20
Cálculo: Limites, Derivadas e Integrais
-
- [Assíntota] - Derivadas
por natanaelskt » Ter Jul 22, 2014 18:40
- 0 Respostas
- 826 Exibições
- Última mensagem por natanaelskt

Ter Jul 22, 2014 18:40
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[3]{6x^2-x^3} \sqrt[3]{6x^2-x^3}](/latexrender/pictures/49c36bfe7d0a2491bf622096f5f68081.png) possui uma assintota oblíqua. Determine a equação dessa assintota e prove que a curva de F(x) intercepta a mesma.
possui uma assintota oblíqua. Determine a equação dessa assintota e prove que a curva de F(x) intercepta a mesma. 
![\sqrt[3]{6x^2-x^3} \sqrt[3]{6x^2-x^3}](/latexrender/pictures/49c36bfe7d0a2491bf622096f5f68081.png) possui uma assintota oblíqua. Determine a equação dessa assintota e prove que a curva de F(x) intercepta a mesma.
possui uma assintota oblíqua. Determine a equação dessa assintota e prove que a curva de F(x) intercepta a mesma. 
possui uma assintota oblíqua. Determine a equação dessa assintota e prove que a curva de F(x) intercepta a mesma.
![F(x)=\sqrt[3]{6x^2-x^3} F(x)=\sqrt[3]{6x^2-x^3}](/latexrender/pictures/4da55a84cfa50c7848e175a63871eeee.png) ou de
ou de ![F(x)=\sqrt[3]{\sqrt[3]{6x^2-x^3}} F(x)=\sqrt[3]{\sqrt[3]{6x^2-x^3}}](/latexrender/pictures/09d1ede9bc8a97fe1b791598be9cb1e3.png) .
. tal que
tal que ![a=\lim_{x\rightarrow \infty} \left[\frac{F(x)}{x}\right] a=\lim_{x\rightarrow \infty} \left[\frac{F(x)}{x}\right]](/latexrender/pictures/8114f1619925b2ea06816fe89aa9b0dd.png) ou
ou ![a=\lim_{x\rightarrow -\infty} \left[\frac{F(x)}{x}\right] a=\lim_{x\rightarrow -\infty} \left[\frac{F(x)}{x}\right]](/latexrender/pictures/7758e468413fda650c3b4d6539e3e6b6.png) e
e ![b=\lim_{x\rightarrow \infty} \left[F(x)-ax\right] b=\lim_{x\rightarrow \infty} \left[F(x)-ax\right]](/latexrender/pictures/14daeaba209f3d3dcbb1f37b49e0e9d0.png) ou
ou ![b=\lim_{x\rightarrow \infty} \left[F(x)-ax\right] b=\lim_{x\rightarrow \infty} \left[F(x)-ax\right]](/latexrender/pictures/14daeaba209f3d3dcbb1f37b49e0e9d0.png) .
.![a=\lim_{x\rightarrow \pm \infty} \left[\frac{\sqrt[3]{6x^2-x^3}}{x}\right]=\lim_{x\rightarrow \pm \infty} \left[\frac{\sqrt[3]{6x^2-x^3}}{\sqrt[3]{x}}\right]=\newline \newline \lim_{x\rightarrow \pm \infty} \left[\sqrt[3]{\frac{6x^2-x^3}{x^3}}\right]=\lim_{x\rightarrow \pm \infty} \left[\sqrt[3]{\frac{6}{x}-1}\right]=-1 a=\lim_{x\rightarrow \pm \infty} \left[\frac{\sqrt[3]{6x^2-x^3}}{x}\right]=\lim_{x\rightarrow \pm \infty} \left[\frac{\sqrt[3]{6x^2-x^3}}{\sqrt[3]{x}}\right]=\newline \newline \lim_{x\rightarrow \pm \infty} \left[\sqrt[3]{\frac{6x^2-x^3}{x^3}}\right]=\lim_{x\rightarrow \pm \infty} \left[\sqrt[3]{\frac{6}{x}-1}\right]=-1](/latexrender/pictures/a50b9f4470ded97fc393230fa23e2434.png)
![b=\lim_{x\rightarrow -\infty} \left[F(x)+ax\right]=\lim_{x\rightarrow -\infty} \left[\sqrt[3]{6x^2-x^3}-(-1)x\right]= b=\lim_{x\rightarrow -\infty} \left[F(x)+ax\right]=\lim_{x\rightarrow -\infty} \left[\sqrt[3]{6x^2-x^3}-(-1)x\right]=](/latexrender/pictures/b491848b03c698ceb63c349342b1c6c0.png)
![=\lim_{x\rightarrow -\infty}\frac{\left[\sqrt[3]{6x^2-x^3}+x\right]\left[(\sqrt[3]{6x^2-x^3})^{2}-x\sqrt[3]{6x^2-x^3}+x^{2}\right]}{\left[(\sqrt[3]{6x^2-x^3})^{2}-x\sqrt[3]{6x^2-x^3}+x^{2}\right]}= =\lim_{x\rightarrow -\infty}\frac{\left[\sqrt[3]{6x^2-x^3}+x\right]\left[(\sqrt[3]{6x^2-x^3})^{2}-x\sqrt[3]{6x^2-x^3}+x^{2}\right]}{\left[(\sqrt[3]{6x^2-x^3})^{2}-x\sqrt[3]{6x^2-x^3}+x^{2}\right]}=](/latexrender/pictures/f0d1216cebab945f018f2a439f75cfe9.png)
![=\lim_{x\rightarrow -\infty}\frac{6x^2}{\left[(\sqrt[3]{6x^2-x^3})^{2}-x\sqrt[3]{6x^2-x^3}+x^{2}\right]}=\frac{6}{3}=2 =\lim_{x\rightarrow -\infty}\frac{6x^2}{\left[(\sqrt[3]{6x^2-x^3})^{2}-x\sqrt[3]{6x^2-x^3}+x^{2}\right]}=\frac{6}{3}=2](/latexrender/pictures/85aac2e0f405555188f86dc4319938be.png)
 usei
usei 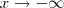 e não
e não 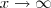 .
.


 , avisa que eu resolvo.
, avisa que eu resolvo.

