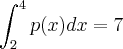 . Podemos concluir que:
. Podemos concluir que:a)
 , para todo x e [2, 4]
, para todo x e [2, 4]b)
 , para todo x e
, para todo x e ![]-\infty, +\infty[ ]-\infty, +\infty[](/latexrender/pictures/cc1790792ccfdf750f3dd0a1e77c869c.png)
c)
 , para algum x e [2, 4]
, para algum x e [2, 4]d)
 , para algum x e [2, 4]
, para algum x e [2, 4]e)
 para todo x e [2,4].
para todo x e [2,4].Creio que essa questão seja relativamente simples, mas confesso que surgiu uma dúvida, primeiro quando olhei essa questão de cara, pensei q a resposta fosse a letra c ou e. Porém, to em duvida de ir logo respondendo de cara. Gostaria de entender o modo como devo resolver essa questão, gostaria de entender o que ha de errado em cada alternativa e o motivo da alternativa correta.
desde já agradeço!


 e
e  de modo que a soma das integrais vale 7 ,i.e, estamos dizemos que p não necessariamente é
de modo que a soma das integrais vale 7 ,i.e, estamos dizemos que p não necessariamente é  em
em ![[2,4] [2,4]](/latexrender/pictures/a157b852663a42e907fc1ae4884ff3e4.png) . Deixo para vc fornecer um contra exemplo .
. Deixo para vc fornecer um contra exemplo .  , absurdo !
, absurdo !  para todo x em
para todo x em  ,absurdo ! .
,absurdo ! .  implica em dizer que para algum x em [2,4] tem-se
implica em dizer que para algum x em [2,4] tem-se  .
.

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)