Não estou conseguindo fazer essas questões:
1) Achar Y'(pi/6) sendo y=[1+sen(x)/cos(x)]
Resp: 2
2) Sendo F(x) = Cos[arcsen(x)] Calcule f'raiz(3)/2
Resp: - Raiz(3)



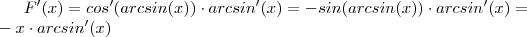 .
.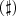 (aqui foi usado que a função seno composta com sua inversa arco seno nos fornece a função identidade e vice-versa )
(aqui foi usado que a função seno composta com sua inversa arco seno nos fornece a função identidade e vice-versa ) 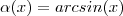 , fazendo seno aplicado a
, fazendo seno aplicado a 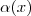 temos
temos 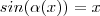 . Derivando-se com respeito a
. Derivando-se com respeito a  tem-se que
tem-se que ![[sin(\alpha (x)) ]' = x' = 1 [sin(\alpha (x)) ]' = x' = 1](/latexrender/pictures/936df7d6866368cab5151b11200a1df2.png) iff
iff 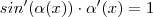 iff
iff 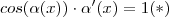 .
. ![[-1,1] [-1,1]](/latexrender/pictures/d060b17b29e0dae91a1cac23ea62281a.png) é lavado ao intervalo
é lavado ao intervalo ![[-\frac{\pi}{2}, \frac{\pi}{2} ] [-\frac{\pi}{2}, \frac{\pi}{2} ]](/latexrender/pictures/20088c2e84017fe5531eea3120563352.png) pela aplicação
pela aplicação  e
e 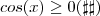 para todo
para todo ![x \in [-\frac{\pi}{2}, \frac{\pi}{2} ] x \in [-\frac{\pi}{2}, \frac{\pi}{2} ]](/latexrender/pictures/c4bc2d2503e158f8255f92e49c13703f.png) . Ocorrendo a igualdade somente quando
. Ocorrendo a igualdade somente quando 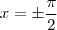 .
.  , vemos que devemos impor que
, vemos que devemos impor que 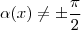 para isto acontecer basta que
para isto acontecer basta que 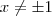 , ou seja ,
, ou seja , 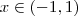 e assim , podemos dividir ambos membros de
e assim , podemos dividir ambos membros de  por
por 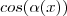 e isto resultará
e isto resultará 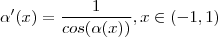 .
. 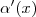 em função apenas de
em função apenas de  , usamos um artificio o qual nos possibilitará estabelecer uma ponte entre seno e cosseno , tal artificio é oriundo da identidade trigonométrica fundamental que diz que
, usamos um artificio o qual nos possibilitará estabelecer uma ponte entre seno e cosseno , tal artificio é oriundo da identidade trigonométrica fundamental que diz que 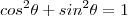 para qualquer que seja
para qualquer que seja  real .
real . 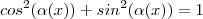 ,ou seja
,ou seja 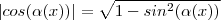 . Que devido a dois fatores já mencionados , vide
. Que devido a dois fatores já mencionados , vide  e
e
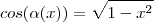 fazendo as devidas substituições encontrará
fazendo as devidas substituições encontrará ![[cos(arcsin(x))]' [cos(arcsin(x))]'](/latexrender/pictures/6de52883bd281033aabcc2018cad41fe.png) . Depois basta fazer
. Depois basta fazer 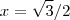 .
. 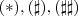 , porém agora de forma sucinta cabendo a vc identificar o emprego deles em cada manipulação ...
, porém agora de forma sucinta cabendo a vc identificar o emprego deles em cada manipulação ... 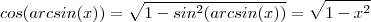 . Logo ,
. Logo , ![[cos(arcsin(x)) ]' = [ \sqrt{1- x^2}]' = ... [cos(arcsin(x)) ]' = [ \sqrt{1- x^2}]' = ...](/latexrender/pictures/e6b7aba9b13bf82968953de713c1a42c.png)

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

