 por Marcos07 » Seg Jun 30, 2014 16:45
por Marcos07 » Seg Jun 30, 2014 16:45
no ponto p = (0,0)
Não estou conseguindo identificar se a função é ou não diferenciável.
Se não tiver compreendido a função, existe uma imagem em anexo abaixo.
- Anexos
-
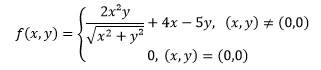
- equação.jpg (7.63 KiB) Exibido 1632 vezes
Editado pela última vez por
Marcos07 em Ter Jul 01, 2014 14:03, em um total de 3 vezes.
-
Marcos07
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Seg Jun 30, 2014 01:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Man Utd » Ter Jul 01, 2014 01:14
por Man Utd » Ter Jul 01, 2014 01:14
Olá

Temos que resolver o "limitão" :
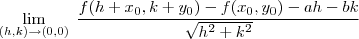
onde
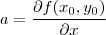
, e ,
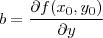
e este "limitão" obrigatoriamente deve ser zero para a função ser diferenciavel no ponto
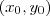
caso não seja feita esta condição a função não é diferenciavél em
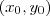
.
Então obtemos que :
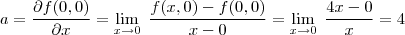
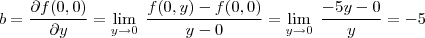
Então :
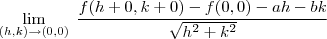
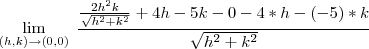
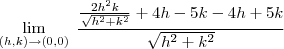
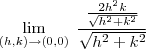
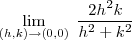
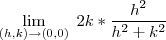
Veja que
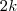
vai a zero quando
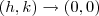
e que
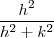
é limitada em
![\left[0,1 \right] \left[0,1 \right]](/latexrender/pictures/7677ea85fbaa1efa02fd80baa7e802de.png)
, para provar isto faça :
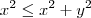
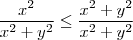
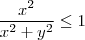
veja tbm que

é sempre positivo , então o menor valor que pode assumir é quando

que implica que
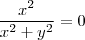
, daí obtemos que esta função é limitada e sua imagem é
![\left[0,1 \right] \left[0,1 \right]](/latexrender/pictures/7677ea85fbaa1efa02fd80baa7e802de.png)
.
Logo pelo teorema da função limitada
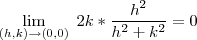
, então como o limite é zero segue que a função
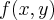
é diferenciavél no ponto
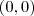
.
Editado pela última vez por
Man Utd em Qua Jul 02, 2014 22:23, em um total de 4 vezes.
-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por Marcos07 » Ter Jul 01, 2014 01:22
por Marcos07 » Ter Jul 01, 2014 01:22
Muito obrigado mesmo. Muito claro e objetivo. nem sabe o quanto me ajudou. valeu mesmo!!!
-
Marcos07
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Seg Jun 30, 2014 01:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ponto em que duas funções se interceptam
por Fernanda Lauton » Dom Jun 13, 2010 18:14
- 7 Respostas
- 7880 Exibições
- Última mensagem por Fernanda Lauton

Seg Jun 14, 2010 16:15
Funções
-
- [Funções diferenciáveis] em um ponto indicado.
 por Marcos07 » Ter Jul 01, 2014 01:55
por Marcos07 » Ter Jul 01, 2014 01:55
- 1 Respostas
- 1168 Exibições
- Última mensagem por Man Utd

Qua Jul 02, 2014 22:00
Cálculo: Limites, Derivadas e Integrais
-
- Ponto em comum entre duas funções
por suziquim » Qui Mai 05, 2011 15:53
- 2 Respostas
- 2409 Exibições
- Última mensagem por suziquim

Qui Mai 05, 2011 17:21
Funções
-
- SE, EM DETERMINADO TRIBUNAL
por vania a » Qua Out 19, 2011 07:54
- 0 Respostas
- 790 Exibições
- Última mensagem por vania a

Qua Out 19, 2011 07:54
Estatística
-
- SE, EM DETERMINADO TRIBUNAL, HA 54 JUIZES
por vania a » Qua Out 19, 2011 07:52
- 1 Respostas
- 1296 Exibições
- Última mensagem por Neperiano

Qua Nov 09, 2011 15:39
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




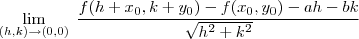 onde
onde 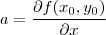 , e ,
, e , 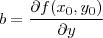 e este "limitão" obrigatoriamente deve ser zero para a função ser diferenciavel no ponto
e este "limitão" obrigatoriamente deve ser zero para a função ser diferenciavel no ponto 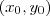 caso não seja feita esta condição a função não é diferenciavél em
caso não seja feita esta condição a função não é diferenciavél em 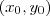 .
.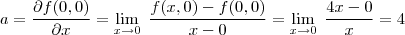
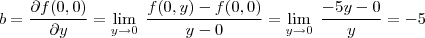
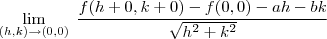
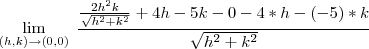
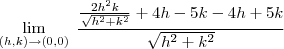
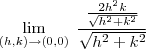
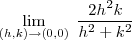
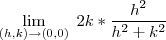
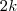 vai a zero quando
vai a zero quando 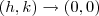 e que
e que 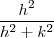 é limitada em
é limitada em ![\left[0,1 \right] \left[0,1 \right]](/latexrender/pictures/7677ea85fbaa1efa02fd80baa7e802de.png) , para provar isto faça :
, para provar isto faça :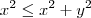
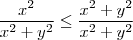
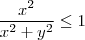
 é sempre positivo , então o menor valor que pode assumir é quando
é sempre positivo , então o menor valor que pode assumir é quando que implica que
que implica que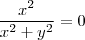 , daí obtemos que esta função é limitada e sua imagem é
, daí obtemos que esta função é limitada e sua imagem é ![\left[0,1 \right] \left[0,1 \right]](/latexrender/pictures/7677ea85fbaa1efa02fd80baa7e802de.png) .
.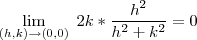 , então como o limite é zero segue que a função
, então como o limite é zero segue que a função 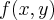 é diferenciavél no ponto
é diferenciavél no ponto 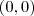 .
.

