 por Janoca » Ter Jun 17, 2014 01:05
por Janoca » Ter Jun 17, 2014 01:05
Com base nesse gráfico que anexei, peço que me ajudem a resolver esta questão;
No intervalo

, o valor médio de f(t),
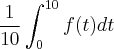
é:
a) entre 0 e 1;
b) 0;
c) entre 0 e -1;
d) g(1);
e) entre -1 e -2.
Não sei como responder.
- Anexos
-
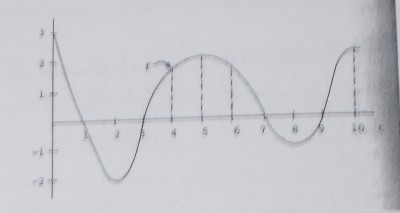
- Gráfico da questão
-
Janoca
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Sex Jun 06, 2014 16:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por alienante » Ter Jun 17, 2014 19:07
por alienante » Ter Jun 17, 2014 19:07
Seja f(c) o velor médio dá função representada pelo gráfico dado
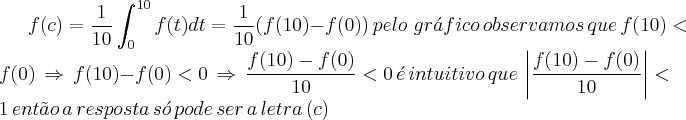
-
alienante
- Usuário Dedicado

-
- Mensagens: 43
- Registrado em: Seg Nov 25, 2013 19:18
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Ter Jun 17, 2014 21:47
por e8group » Ter Jun 17, 2014 21:47
Se me permitem participar ; analisando o gráfico consegui obter um limitante inferior para integral
(levando em conta que o raciocínio estar certo ) . Infelizmente perdi a conexão com a internet e o que eu tinha feito perdi .
Então , segue uma dica :
Decomponha a integral em soma de integrais,sendo cada uma delas sobre um dos intervalos
![[0,1] ; [1,3] ; [3,7] ; [7,9] [0,1] ; [1,3] ; [3,7] ; [7,9]](/latexrender/pictures/a1399b15beac5a65e106b28407e3e8c8.png)
e
![[9,10] [9,10]](/latexrender/pictures/161d392c82c6c3fa93f611bd9284b6b6.png)
.
No primeiro intervalo , note que a área do triângulo retângulo (base medindo 1/2 e altura 3 ) que é
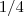
é menor que a integral de f(x) sobre o mesmo intervalo ; no segundo (compare por área de retângulo ) ,
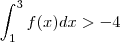
; no terceiro (compare por área de trapézio ) ,
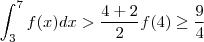
; no quarto (compare por área de retângulo )
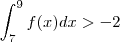
e no último (compare com área de triângulo )
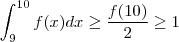
.
Somando-se obterá o limitante inferior 0.25 .
Resumidamente foi nesta linha que trabelhei .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Janoca » Qua Jun 18, 2014 13:15
por Janoca » Qua Jun 18, 2014 13:15
A resposta certa não seria a letra a? ao inves da c.
-
Janoca
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Sex Jun 06, 2014 16:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por alienante » Qua Jun 18, 2014 14:07
por alienante » Qua Jun 18, 2014 14:07
concorda comigo que pelo gráfico f(10)<f(0)? logo f(10)-f(0)<0, só seria a letra a se e somente se f(10)-f(0)>0
-
alienante
- Usuário Dedicado

-
- Mensagens: 43
- Registrado em: Seg Nov 25, 2013 19:18
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Janoca » Qua Jun 18, 2014 14:59
por Janoca » Qua Jun 18, 2014 14:59
Concordo! Obrigada
-
Janoca
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Sex Jun 06, 2014 16:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por e8group » Qua Jun 18, 2014 15:34
por e8group » Qua Jun 18, 2014 15:34
Caro , alienante . Acho que você está equivocado , não está ? Ou eu estou raciocinando erroneamente ??
" concorda comigo que pelo gráfico f(10)<f(0)? logo f(10)-f(0)<0, só seria a letra a se e somente se f(10)-f(0)> 0"
Isto é falso . Contra-exemplo :
Defina
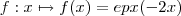
. Nós temos
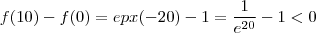
, mas !
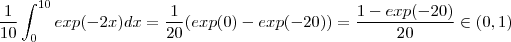
.
No mínimo a integral requerida está entre
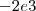
, pois vê-se no gráfico que a função é limitada inferiormente por
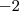
e superiormente por

e a integral cumpre com a monotonicidade .
Até aqui , os itens que fazem sentido são as letras

e
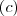
entretanto , pelo post acima visto que a integral é limitada inferiormente por um n° entre zero e 1 ; logo só pode ser (a) .
Para frisar o que estou dizendo vou deixar a imagem anexada , compare a integral com a área dos retângulos , triângulos e trapézios .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por alienante » Qua Jun 18, 2014 18:11
por alienante » Qua Jun 18, 2014 18:11
De fato, percebi agora meu erro, obrigado por me corrigir santhiago
-
alienante
- Usuário Dedicado

-
- Mensagens: 43
- Registrado em: Seg Nov 25, 2013 19:18
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [VALOR MÉDIO]
por magellanicLMC » Sex Fev 07, 2014 23:05
- 2 Respostas
- 1689 Exibições
- Última mensagem por magellanicLMC

Sáb Fev 08, 2014 17:00
Cálculo: Limites, Derivadas e Integrais
-
- teorema do valor medio
por matmatco » Seg Nov 14, 2011 10:18
- 3 Respostas
- 2684 Exibições
- Última mensagem por LuizAquino

Seg Nov 14, 2011 20:46
Cálculo: Limites, Derivadas e Integrais
-
- Teorema do valor médio
por crsjcarlos » Qua Mai 01, 2013 12:09
- 1 Respostas
- 1997 Exibições
- Última mensagem por e8group

Qua Mai 01, 2013 14:07
Cálculo: Limites, Derivadas e Integrais
-
- [teorema do valor médio]
por Ge_dutra » Seg Jun 17, 2013 00:12
- 0 Respostas
- 1222 Exibições
- Última mensagem por Ge_dutra

Seg Jun 17, 2013 00:12
Cálculo: Limites, Derivadas e Integrais
-
- Duvida teorema do valor médio
por markitodq » Dom Abr 21, 2013 09:47
- 0 Respostas
- 1223 Exibições
- Última mensagem por markitodq

Dom Abr 21, 2013 09:47
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , o valor médio de f(t),
, o valor médio de f(t), 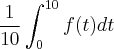 é:
é:
 , o valor médio de f(t),
, o valor médio de f(t), 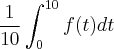 é:
é:
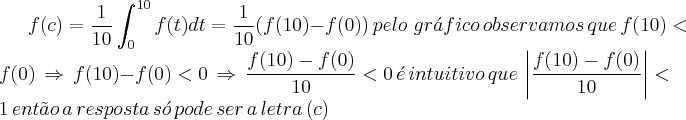

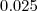 (levando em conta que o raciocínio estar certo ) . Infelizmente perdi a conexão com a internet e o que eu tinha feito perdi .
(levando em conta que o raciocínio estar certo ) . Infelizmente perdi a conexão com a internet e o que eu tinha feito perdi . ![[0,1] ; [1,3] ; [3,7] ; [7,9] [0,1] ; [1,3] ; [3,7] ; [7,9]](/latexrender/pictures/a1399b15beac5a65e106b28407e3e8c8.png) e
e ![[9,10] [9,10]](/latexrender/pictures/161d392c82c6c3fa93f611bd9284b6b6.png) .
. 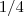 é menor que a integral de f(x) sobre o mesmo intervalo ; no segundo (compare por área de retângulo ) ,
é menor que a integral de f(x) sobre o mesmo intervalo ; no segundo (compare por área de retângulo ) , 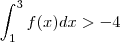 ; no terceiro (compare por área de trapézio ) ,
; no terceiro (compare por área de trapézio ) , 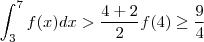 ; no quarto (compare por área de retângulo )
; no quarto (compare por área de retângulo ) 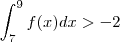 e no último (compare com área de triângulo )
e no último (compare com área de triângulo ) 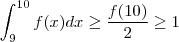 .
. 



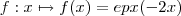 . Nós temos
. Nós temos 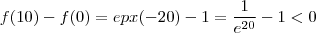 , mas !
, mas ! 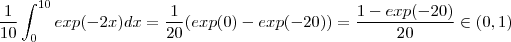 .
. 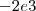 , pois vê-se no gráfico que a função é limitada inferiormente por
, pois vê-se no gráfico que a função é limitada inferiormente por 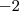 e superiormente por
e superiormente por  e a integral cumpre com a monotonicidade .
e a integral cumpre com a monotonicidade .  e
e 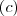 entretanto , pelo post acima visto que a integral é limitada inferiormente por um n° entre zero e 1 ; logo só pode ser (a) .
entretanto , pelo post acima visto que a integral é limitada inferiormente por um n° entre zero e 1 ; logo só pode ser (a) . 
