Proposição :
Se

é uma função impar integrável em um intervalo fechado cujos os extremos do intervalo são números simétricos , então a integral de f sobre este intervalo vale zero .
Lembrando que f é impar se ocorrer x ,-x estão em Dom(f) e f(x) = -f(-x) .
Por simplicidade , vamos "chamar" a própria regra de associação ou lei de formação , da função f , de função . Assim, vamos dizer a função f(x) ...
Do integrando , a segunda e as duas ultimas 'funções ' são impares (em ordem da esquerda para a direita)[deixo vc verificar este fato !] e estas 'funções ' são continuas no intervalo
![[-3,3] [-3,3]](/latexrender/pictures/083d33f8040330c3051e16ce69a5b0df.png)
e portanto integrável sobre este intervalo .Graças a proposição acima , o integral sobre
![[-3,3] [-3,3]](/latexrender/pictures/083d33f8040330c3051e16ce69a5b0df.png)
destas 'funções ' valem zero . Usando a linearidade da integral , as contas se resumem a
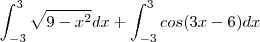
.
Consegue avançar ??


 é uma função impar integrável em um intervalo fechado cujos os extremos do intervalo são números simétricos , então a integral de f sobre este intervalo vale zero .
é uma função impar integrável em um intervalo fechado cujos os extremos do intervalo são números simétricos , então a integral de f sobre este intervalo vale zero . ![[-3,3] [-3,3]](/latexrender/pictures/083d33f8040330c3051e16ce69a5b0df.png) e portanto integrável sobre este intervalo .Graças a proposição acima , o integral sobre
e portanto integrável sobre este intervalo .Graças a proposição acima , o integral sobre 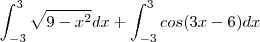 .
.

 .
.



