Dica para calcular limites de funções racionais (razão de polinômios )
Queremos computar limites de funções racionais :
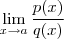
.
Primeiramente , certifique-se

é raiz de
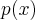 e
e 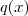
.Isto é , se
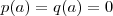
.
Se isto acima
não ocorrer , não teremos indeterminação (0/0) e assim o calculo do limite segue diretamente pela regra do quociente . Possa ser que este limite seja finito ou não .
Agora suponha que a situação descrita acima ocorra .
Neste caso, podemos reescrever cada polinômio como expressões da forma
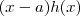
( onde
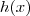
é um polinômio ) que por conseguinte os fatores em comum se cancelam no calculo do limite . Após esta etapa , caímos novamente no problema de computar limites de funções racionais . E novamente fazemos a mesma verificação .
Para reescrever um dos polinômios como
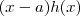
em geral dividimos ele por

. Porém não é a único modo embora mais comum .
É possível fatorar
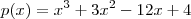
sem o método da divisão também , bem como você quiser .
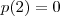
.
E
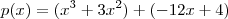
.
Os termos entre parêntesis avaliados em x = 2 são diferentes de zero (mas soma deles zero , certo ?) .
A saber ,
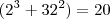
e
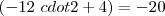
.
Soma-se então
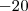
em
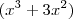
e
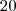
em
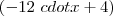
, desta forma ambas parcelas zeraram em x = 2 e terão o mesmo fator x-2 em comum que poderemos deixá-ló em evidência . Além disso , a igualdade permanece
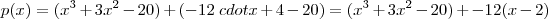
.
E também (fazendo manipulações análogas com o mesmo objetivo )
![(x^3 + 3 x^2 - 20) = (x^2[x +3 ] - 20) = (x^2[x -2 + 5 ] -20) = (x^2[x-2] + 5x^2 -20) = (x^2[x-2] + 5[x^2 -4]) (x^3 + 3 x^2 - 20) = (x^2[x +3 ] - 20) = (x^2[x -2 + 5 ] -20) = (x^2[x-2] + 5x^2 -20) = (x^2[x-2] + 5[x^2 -4])](/latexrender/pictures/e3db09578dadd391734846378f72ccb7.png)
.
Porém sabemos que
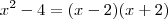
. E com isso
![(x^2[x-2] + 5[x^2 -4]) = (x^2[x-2] + 5[x-2][x+2]) = [x-2](x^2 +5x +10) (x^2[x-2] + 5[x^2 -4]) = (x^2[x-2] + 5[x-2][x+2]) = [x-2](x^2 +5x +10)](/latexrender/pictures/8741eed1efa158b7d68e77e1d8ce4737.png)
.
Juntando os resultados
 -12[x -2] = [x-2](x^2 +5x + 34) (x^3 + 3 x^2 - 20 ) -12(x -2) = [x-2](x^2 +5x +10) -12[x -2] = [x-2](x^2 +5x + 34)](/latexrender/pictures/99cbbef47d32eeccfb18b0fbf31bc23a.png)
e
Quanto o denominador mais simples .
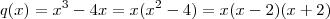
Logo
}{x(x-2)(x+2)} = \lim_{x\to 2} \frac{x^2 +5x + 34}{x(x+2)} \lim_{x\to 2} \frac{p(x)}{q(x)} = \lim_{x\to 2} \frac{[x-2](x^2 +5x + 34)}{x(x-2)(x+2)} = \lim_{x\to 2} \frac{x^2 +5x + 34}{x(x+2)}](/latexrender/pictures/24cad79f1bc009d988ae1eb0e9ff2681.png)
(pois x tende a 2 , x não é igual a 2) .
Vale ressaltar que nem sempre é simples reescrever polinômios em sua forma fatorada sem a divisão do mesmo por

.Portanto , o método é mais recomendado .
Uma formula útil :
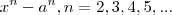
Divida
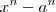
por

para obter uma fórmula que escrita na forma compacta de soma (ajuda a memorização da mesma ) é
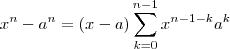
.
Aceitando que a formula é verdadeira ,temos
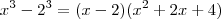
.
Em consequência , temos outra forma de fatorar p ,
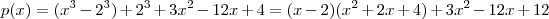
Agora
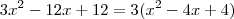
.
É fácil calcular as raízes eq. segundo grau , uma já sabemos q é

e a outra podemos ver que também é 2 , multiplicidade 2 , pois
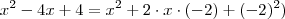
que é o desenvolvimento de
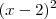
. Logo ,
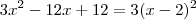
Juntamos o que temos
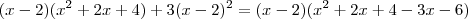
.
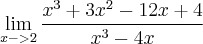


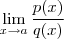 .
.  é raiz de
é raiz de 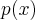
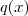 .Isto é , se
.Isto é , se 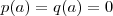 .
. 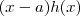 ( onde
( onde 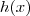 é um polinômio ) que por conseguinte os fatores em comum se cancelam no calculo do limite . Após esta etapa , caímos novamente no problema de computar limites de funções racionais . E novamente fazemos a mesma verificação .
é um polinômio ) que por conseguinte os fatores em comum se cancelam no calculo do limite . Após esta etapa , caímos novamente no problema de computar limites de funções racionais . E novamente fazemos a mesma verificação . . Porém não é a único modo embora mais comum .
. Porém não é a único modo embora mais comum . 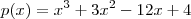 sem o método da divisão também , bem como você quiser .
sem o método da divisão também , bem como você quiser .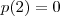 .
. 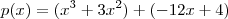 .
. 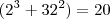 e
e 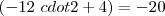 .
. 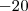 em
em 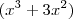 e
e 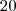 em
em 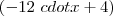 , desta forma ambas parcelas zeraram em x = 2 e terão o mesmo fator x-2 em comum que poderemos deixá-ló em evidência . Além disso , a igualdade permanece
, desta forma ambas parcelas zeraram em x = 2 e terão o mesmo fator x-2 em comum que poderemos deixá-ló em evidência . Além disso , a igualdade permanece 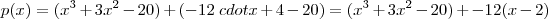 .
. ![(x^3 + 3 x^2 - 20) = (x^2[x +3 ] - 20) = (x^2[x -2 + 5 ] -20) = (x^2[x-2] + 5x^2 -20) = (x^2[x-2] + 5[x^2 -4]) (x^3 + 3 x^2 - 20) = (x^2[x +3 ] - 20) = (x^2[x -2 + 5 ] -20) = (x^2[x-2] + 5x^2 -20) = (x^2[x-2] + 5[x^2 -4])](/latexrender/pictures/e3db09578dadd391734846378f72ccb7.png) .
. 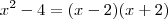 . E com isso
. E com isso ![(x^2[x-2] + 5[x^2 -4]) = (x^2[x-2] + 5[x-2][x+2]) = [x-2](x^2 +5x +10) (x^2[x-2] + 5[x^2 -4]) = (x^2[x-2] + 5[x-2][x+2]) = [x-2](x^2 +5x +10)](/latexrender/pictures/8741eed1efa158b7d68e77e1d8ce4737.png) .
.  -12[x -2] = [x-2](x^2 +5x + 34) (x^3 + 3 x^2 - 20 ) -12(x -2) = [x-2](x^2 +5x +10) -12[x -2] = [x-2](x^2 +5x + 34)](/latexrender/pictures/99cbbef47d32eeccfb18b0fbf31bc23a.png) e
e 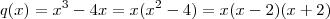
}{x(x-2)(x+2)} = \lim_{x\to 2} \frac{x^2 +5x + 34}{x(x+2)} \lim_{x\to 2} \frac{p(x)}{q(x)} = \lim_{x\to 2} \frac{[x-2](x^2 +5x + 34)}{x(x-2)(x+2)} = \lim_{x\to 2} \frac{x^2 +5x + 34}{x(x+2)}](/latexrender/pictures/24cad79f1bc009d988ae1eb0e9ff2681.png) (pois x tende a 2 , x não é igual a 2) .
(pois x tende a 2 , x não é igual a 2) . .Portanto , o método é mais recomendado .
.Portanto , o método é mais recomendado .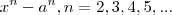
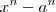 por
por 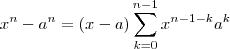 .
. 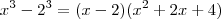 .
.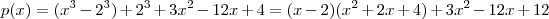
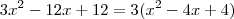 .
.  e a outra podemos ver que também é 2 , multiplicidade 2 , pois
e a outra podemos ver que também é 2 , multiplicidade 2 , pois 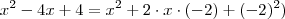 que é o desenvolvimento de
que é o desenvolvimento de 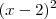 . Logo ,
. Logo , 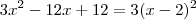
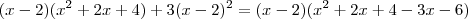 .
.
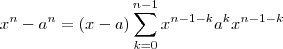 que de fácil memorização .Com isso ganhamos praticidade na fatoração de expressões como
que de fácil memorização .Com isso ganhamos praticidade na fatoração de expressões como 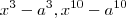 e etc . A motivação é o polinômio de grau
e etc . A motivação é o polinômio de grau  incompleto , o coeficiente
incompleto , o coeficiente  e os demais
e os demais 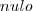 . Isto é ,
. Isto é , 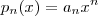 .
. 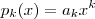 com
com 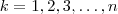 .
. 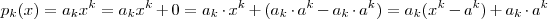 .Porém sabemos que ,
.Porém sabemos que , 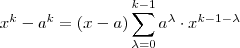 .
. 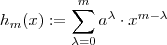 .
. 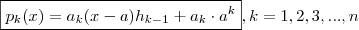 .
. 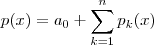 que devido a fórmula destacada ,
que devido a fórmula destacada , 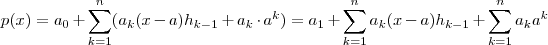 ou ainda
ou ainda 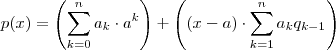 .
. 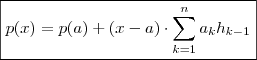 onde
onde 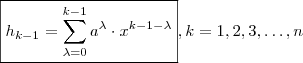 .
.  . Isto nos fornece uma formula prática para fatorar polinômios , quando sabemos uma de suas raízes (especialmente polinômios de grau maior que 2) .
. Isto nos fornece uma formula prática para fatorar polinômios , quando sabemos uma de suas raízes (especialmente polinômios de grau maior que 2) . 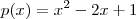 , verificamos que
, verificamos que 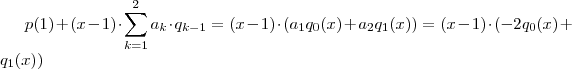
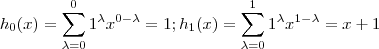
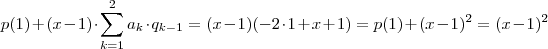
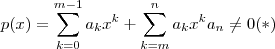 com
com 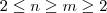 .Defina também ,
.Defina também , 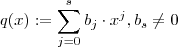 com
com 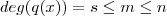 .
. 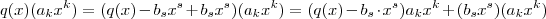 com
com  . Dividindo todos os termos por
. Dividindo todos os termos por 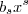 ( a princípio suponha
( a princípio suponha  )
)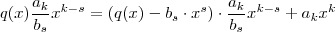 com isso concluímos que
com isso concluímos que 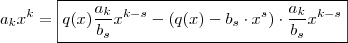 . (
. (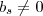 por hipótese ) .
por hipótese ) .  pois
pois  .
.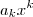 com
com 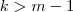 pela fórmula correspondente ,
pela fórmula correspondente , ![p(x) = \sum_{k=0}^{m-1} a_k x^k + \sum_{k=m}^n \left(q(x) \frac{a_k}{b_s} x^{k-s} - (q(x) - b_s \cdot x^s)\cdot \frac{a_k}{b_s} x^{k-s} \right) \iff
[tex] p(x) = \sum_{k=0}^{m-1} a_k x^k -\sum_{k=m}^n \frac{a_k}{b_s} \cdot (q(x) - b_s \cdot x^s)\cdot x^{k-s} \right) + q(x) \sum_{k=m}^n \frac{a_k}{b_s} x^{k-s} p(x) = \sum_{k=0}^{m-1} a_k x^k + \sum_{k=m}^n \left(q(x) \frac{a_k}{b_s} x^{k-s} - (q(x) - b_s \cdot x^s)\cdot \frac{a_k}{b_s} x^{k-s} \right) \iff
[tex] p(x) = \sum_{k=0}^{m-1} a_k x^k -\sum_{k=m}^n \frac{a_k}{b_s} \cdot (q(x) - b_s \cdot x^s)\cdot x^{k-s} \right) + q(x) \sum_{k=m}^n \frac{a_k}{b_s} x^{k-s}](/latexrender/pictures/3f694f2b5b9ae0fb5ca8a027d7bfb752.png) .
. 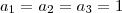 e
e 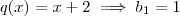 .
. ![q(x) \frac{a_k}{b_s} x^{k-s} - (q(x) - b_s \cdot x^s)\cdot \frac{a_k}{b_s} x^{k-s} } = a_n [tex]
[tex] a_1 x = (x+2) - 2 \cdot 1 q(x) \frac{a_k}{b_s} x^{k-s} - (q(x) - b_s \cdot x^s)\cdot \frac{a_k}{b_s} x^{k-s} } = a_n [tex]
[tex] a_1 x = (x+2) - 2 \cdot 1](/latexrender/pictures/97e062f0927cd0f4a51a5cb123f0b6a3.png)
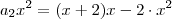
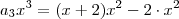
![\sum_{i=1}^3 a_i x^i = (x+2)[1 +x + x^2] - 2 - 2x^2 - 2x^2 = (x+2)[1 +x + x^2]+ -2 -4x^2 \sum_{i=1}^3 a_i x^i = (x+2)[1 +x + x^2] - 2 - 2x^2 - 2x^2 = (x+2)[1 +x + x^2]+ -2 -4x^2](/latexrender/pictures/a2964147cb55072d3ea6e067e1c75d2d.png) .
.  todos termos
todos termos 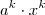 são também dividido. A ideia é escrever cada termo como
são também dividido. A ideia é escrever cada termo como 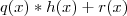 e foi isso que fizemos .
e foi isso que fizemos .  dividido por
dividido por  implica que
implica que 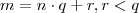 .
.