Boa tarde,
Tenho uma dúvida no exercício 13, e gostava que alguém me explicasse como se faz:
http://postimg.org/image/b9hzq643z/
(O exercício encontrasse neste site)
Obrigado
Luís Soares



 ,
, 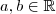 . Sabemos que, se essa reta é tangente ao gráfico de
. Sabemos que, se essa reta é tangente ao gráfico de  no ponto
no ponto  , então
, então .
. é a derivada da função calculada no ponto de tangência.
é a derivada da função calculada no ponto de tangência.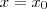 temos de ter
temos de ter  , então
, então

 no ponto
no ponto 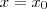 .
. em
em  então, por comparação,
então, por comparação,
 e
e  .
. de onde
de onde  . OBS: este
. OBS: este  e
e  não tem nada que ver com a dedução da equação da reta tangente que fizemos anteriormente.
não tem nada que ver com a dedução da equação da reta tangente que fizemos anteriormente. 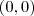 , então
, então  .
.

 em
em  e
e  . Podemos resolve-lo de diversas formas. Eu acho mais rápido somar as duas equações, já que o coeficiente de
. Podemos resolve-lo de diversas formas. Eu acho mais rápido somar as duas equações, já que o coeficiente de  automaticamente se cancela. Fazendo isso,
automaticamente se cancela. Fazendo isso,
 .
.

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

