Materiais sobre Cálculo.
Utilize a seção de pedidos para outros que não estejam disponíveis.
As fontes dos arquivos serão diversas e deverão ser citadas sempre que possível, mantendo totalmente os créditos dos respectivos autores.
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por braddock » Seg Mai 05, 2014 04:06
por braddock » Seg Mai 05, 2014 04:06
Estou tendo um problema no seguinte limite, x e y tendem a 0, sei que o limite vai dar zero, mas não consigo resolver... se alguém conseguir me ajudar, ficaria grato
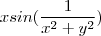
-
braddock
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Mai 05, 2014 03:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Eletrônica
- Andamento: cursando
 por e8group » Seg Mai 05, 2014 10:59
por e8group » Seg Mai 05, 2014 10:59
Dica :
Limite de funções da forma que ( u * v ) é zero sempre que uma delas é limitada e o limite da outra é zero .
Sejam
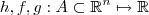
. Defina
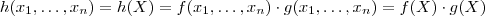
. Suponha

limitada , isto é , existe algum

tal que
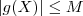
para qualquer que seja o vetor

em

.
Se para algum
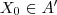
, temos
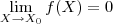
então
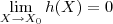
.
(

representa o conjunto dos ponto de acumulação de A)
De fato ,
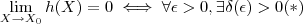
tal que se
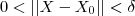
então

.
Segue-se que

.
Além disso , por hipótese
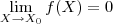
, o que significa que dado

existe um

(correspondente) tal que
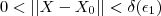
implica

.
Logo ,
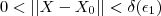
implica
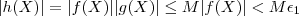
.
Como a relação acima é verdadeira para qualquer

, dado
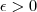
podemos tomar
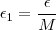
e com isso temos
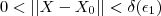
implica

.
Ou seja, dado
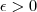
, tomando

conseguimos um
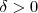
tal que se (o lardo esquerdo da implicação é verdeiro o lado direito também o é )
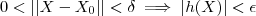
.
É o que exatamente diz em
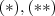
.
Agora com absoluta certeza podemos afirmar que

.
Espero que ajude .
Para exemplificar
Seja

(onde :
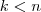
)
Temos que
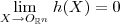
( onde
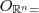
vetor nulo do R^n ) , pois
como
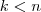
, então
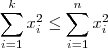
e assim

. Seja

e

.
Temos que g é limitada (por 1) e o limite de f é zero quando X tende ao vetor nulo , logo o limite de h também é zero .
Mais um exemplo ...
Se
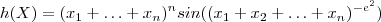
. Temos

(Pq ??)
Espero que ajude .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por braddock » Seg Mai 05, 2014 22:17
por braddock » Seg Mai 05, 2014 22:17
Ajudou muito sim, muito obrigado.
-
braddock
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Mai 05, 2014 03:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Eletrônica
- Andamento: cursando
Voltar para Cálculo
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4792 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite]Limite de uma funçao de varias variaveis
por TheKyabu » Seg Fev 04, 2013 22:01
- 3 Respostas
- 3469 Exibições
- Última mensagem por young_jedi

Ter Fev 05, 2013 19:47
Cálculo: Limites, Derivadas e Integrais
-
- Derivada com várias variáveis
por kryzay » Seg Mai 14, 2012 09:23
- 2 Respostas
- 2675 Exibições
- Última mensagem por kryzay

Seg Mai 14, 2012 10:58
Cálculo: Limites, Derivadas e Integrais
-
- [Derivação Implícita] Várias Variáveis
 por Bob90 » Ter Abr 09, 2013 07:52
por Bob90 » Ter Abr 09, 2013 07:52
- 0 Respostas
- 2317 Exibições
- Última mensagem por Bob90

Ter Abr 09, 2013 07:52
Cálculo: Limites, Derivadas e Integrais
-
- Limites de funções com varias variáveis
por Fernandobertolaccini » Qua Dez 17, 2014 10:49
- 1 Respostas
- 3759 Exibições
- Última mensagem por Molina

Qua Dez 17, 2014 13:59
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
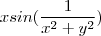


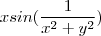

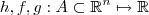 . Defina
. Defina 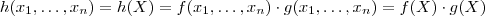 . Suponha
. Suponha  limitada , isto é , existe algum
limitada , isto é , existe algum  tal que
tal que 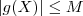 para qualquer que seja o vetor
para qualquer que seja o vetor  em
em  .
. 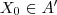 , temos
, temos 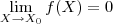 então
então 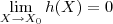 .
. representa o conjunto dos ponto de acumulação de A)
representa o conjunto dos ponto de acumulação de A) 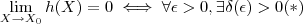 tal que se
tal que se 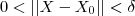 então
então  .
.  .
. 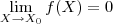 , o que significa que dado
, o que significa que dado  existe um
existe um  (correspondente) tal que
(correspondente) tal que 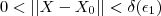 implica
implica  .
. 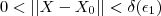 implica
implica 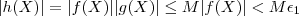 .
.  , dado
, dado 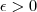 podemos tomar
podemos tomar 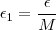 e com isso temos
e com isso temos 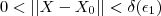 implica
implica  .
. 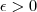 , tomando
, tomando  conseguimos um
conseguimos um 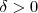 tal que se (o lardo esquerdo da implicação é verdeiro o lado direito também o é )
tal que se (o lardo esquerdo da implicação é verdeiro o lado direito também o é ) 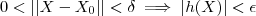 .
. 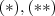 .
.  .
.  (onde :
(onde : 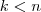 )
)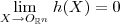 ( onde
( onde 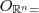 vetor nulo do R^n ) , pois
vetor nulo do R^n ) , pois 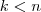 , então
, então 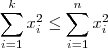 e assim
e assim  . Seja
. Seja  e
e  .
. 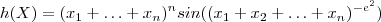 . Temos
. Temos  (Pq ??)
(Pq ??) 
