FAP0151
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
por ARCS » Seg Set 24, 2012 21:36
Peço ajuda de vocÊs nesta questão:
Determine o ângulo para o qual a tração é menor possível:
http://imageshack.us/f/14/p44mc.jpg/a) cabo BC. Resposta alfa = 35
b) simultaneamente nos dois cabos. Resposta alfa = 55
somado as resultantes das forças em cada eixo:
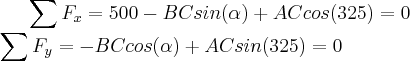
Para resolver a item (a) eu derivei BC implicitamente em relação a alfa e considerei AC como uma constante, mas não encontrei o resultado correto.
E o item (b) eu não tenha ideia nenhuma de como se faz.
-
ARCS
- Usuário Dedicado
-
- Mensagens: 40
- Registrado em: Qui Out 28, 2010 18:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
por Neperiano » Ter Out 09, 2012 10:09
Olá
Montando os somatórios em x e em y.
500-TACcos35-TBCsen.alfa=0
TACcos55-TBCcosalfa=0
Agora faça uma adição, ou substituição, irá dar tangente de alfa = 500, ai você consegue descubrir o valor do angulo.
Att
Sómente os mortos conhecem o fim da guerra
"Platão"
-
Neperiano
- Colaborador Voluntário
-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
por lucasdemirand » Ter Abr 22, 2014 19:13
olá amigo, apenas uma duvida que fiquei em relaçao ao exercicio. Ao calcular tangente de alfa = 500. pela calculadora encontrasse o angulo para alfa de aproximadamente 90 graus. no entanto a resposta pelo gabarito é de 35, isso se deve a uma diminuiçao de 90 por 55 ( angulo indicado no exercicio) certo ?
-
lucasdemirand
- Usuário Dedicado
-
- Mensagens: 31
- Registrado em: Sáb Jul 06, 2013 12:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica
- Andamento: cursando
Voltar para Fundamentos de Mecânica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- duvida estatica
por xiko » Ter Set 14, 2010 10:03
- 3 Respostas
- 2148 Exibições
- Última mensagem por xiko
Dom Set 19, 2010 17:42
Trigonometria
-
- Problema de Minimização
por ARCS » Qui Mai 03, 2012 01:55
- 1 Respostas
- 3177 Exibições
- Última mensagem por LuizAquino
Qui Mai 03, 2012 10:10
Cálculo: Limites, Derivadas e Integrais
-
- Problema de Minimização de Custos
por Fernandobertolaccini » Ter Out 28, 2014 21:54
- 0 Respostas
- 966 Exibições
- Última mensagem por Fernandobertolaccini
Ter Out 28, 2014 21:54
Cálculo: Limites, Derivadas e Integrais
-
- Minimização e zeros um traço de uma matriz
por GoodSpirit » Qui Jan 24, 2013 11:42
- 1 Respostas
- 2099 Exibições
- Última mensagem por GoodSpirit
Sex Jan 25, 2013 13:27
Matrizes e Determinantes
-
- Dúvida de Prob.
por RJ1572 » Seg Mai 24, 2010 11:20
- 1 Respostas
- 1386 Exibições
- Última mensagem por Lucio Carvalho
Seg Mai 24, 2010 15:58
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:
Então pense o seguinte: a fração geratriz de 0,05 é
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,
da seguinte forma:
.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,
da seguinte forma:
.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
