Nesse tipo de exercício o caminho certo é
equacionar as informações. Isto é, "traduza" para matemática todas as sentenças no enunciado.
Você tem 3 funcionário: E, F e D. Aqui, o próprio enunciado já começa a traduzir para linguagem matemática o problema( a menos que você já tenha visto alguém se chamar "E","F" ou "D").
IzabelHeloisa escreveu:"E" ganha 30% mais do que "D"
Para equacionar essa informação precisamos supor que sabemos quanto ganha E e F. Como fazemos isso? Álgebra! Diga que E ganha
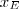
e D ganha
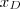
. Pronto. A frase se traduz para:
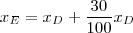
ou
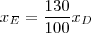
.
Certo? Se sim, vamos prosseguir.
IzabelHeloisa escreveu:e "F", 10% menos que "E"
Esta sentença se traduz da mesma forma que a anterior. Com o detalhe de que , agora, o funcionário da esquerda ganha MENOS que o da direita.
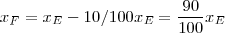
A última sentença
IzabelHeloisa escreveu: três recebem, no fim do mês, R$ 4.858,00.
é a mais simples.
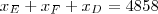
Nesta, basta substituir as relações que encontramos antes. Por exemplo, vamos calcular primeiro
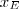
. Já temos a relação de
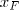
com
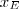
. Agora, manipulando a 1° relação que obtivemos vem que
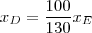
. Daí,
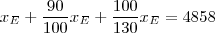
de onde você deve calcular
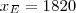
. E, portanto, também deve calcular
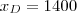
e
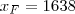
.


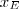 e D ganha
e D ganha 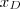 . Pronto. A frase se traduz para:
. Pronto. A frase se traduz para: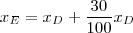
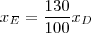 .
.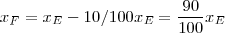
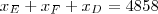
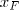 com
com 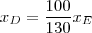 . Daí,
. Daí,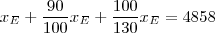
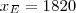 . E, portanto, também deve calcular
. E, portanto, também deve calcular 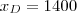 e
e 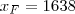 .
.
