 por martinscairo » Sex Abr 18, 2014 16:49
por martinscairo » Sex Abr 18, 2014 16:49
Defina o limite de (3x²)/[1-cos²(x/2)] quando x->0
-
martinscairo
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Abr 18, 2014 16:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por e8group » Seg Abr 21, 2014 12:34
por e8group » Seg Abr 21, 2014 12:34
Você quer apenas computar o limite ? Ou Provar via definição formal ?
De qualquer forma , introduzimos mudança de variável , podemos deixar
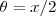
.Quando
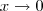
temos
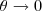
e a nova expressão fica como
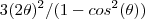
, ou ainda , usando a relação trigonométrica fundamental , resulta
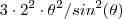
. Agora só + algumas manipulações de modo a usar o limite fundamental .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limites] Limites pela definiçao
 por JoaoLuiz07 » Qui Ago 27, 2015 16:55
por JoaoLuiz07 » Qui Ago 27, 2015 16:55
- 1 Respostas
- 1768 Exibições
- Última mensagem por adauto martins

Sáb Ago 29, 2015 20:52
Cálculo: Limites, Derivadas e Integrais
-
- Limites por definição em R2
por Saruman » Ter Abr 27, 2010 16:26
- 1 Respostas
- 2527 Exibições
- Última mensagem por Neperiano

Ter Set 27, 2011 19:55
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Definição
 por felipe10 » Qui Mai 03, 2012 18:46
por felipe10 » Qui Mai 03, 2012 18:46
- 3 Respostas
- 3538 Exibições
- Última mensagem por LuizAquino

Sex Mai 04, 2012 18:41
Cálculo: Limites, Derivadas e Integrais
-
- Limites por definição.
 por lucassouza » Qui Jan 29, 2015 18:50
por lucassouza » Qui Jan 29, 2015 18:50
- 1 Respostas
- 1358 Exibições
- Última mensagem por adauto martins

Sáb Jan 31, 2015 18:31
Cálculo: Limites, Derivadas e Integrais
-
- Limites pela definição
por Fred Pellegrini » Sex Out 28, 2016 18:21
- 1 Respostas
- 4671 Exibições
- Última mensagem por adauto martins

Seg Out 31, 2016 10:14
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



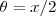 .Quando
.Quando 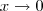 temos
temos 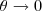 e a nova expressão fica como
e a nova expressão fica como 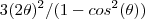 , ou ainda , usando a relação trigonométrica fundamental , resulta
, ou ainda , usando a relação trigonométrica fundamental , resulta 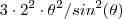 . Agora só + algumas manipulações de modo a usar o limite fundamental .
. Agora só + algumas manipulações de modo a usar o limite fundamental .

 .
.



