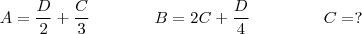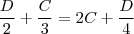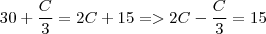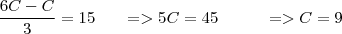por israel jonatas » Seg Dez 02, 2013 12:08
por israel jonatas » Seg Dez 02, 2013 12:08
Quatro amigos, Abel, Bruno, Caio e Daniel, são colecionadores de figurinhas. Sabe-se que Abel possui metade da quantidade de figurinha de Daniel mais um terço da quantidade de figurinhas de Caio; que Bruno possui o dobro da quantidade de Caio mais quarta parte da quantidade de figurinhas de Daniel; que Daniel tem 60 figurinhas, e que Abel e Bruno possuem a mesma quantidade de figurinhas. Os quatro amigos possuem, juntos:
a) 125
b) 128
c) 130
d) 132
e) 135
-
israel jonatas
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Mar 14, 2013 13:04
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
-
Iniciante
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Mar 28, 2014 18:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por israel jonatas » Sáb Abr 19, 2014 11:10
por israel jonatas » Sáb Abr 19, 2014 11:10
Iniciante escreveu:Considerando: Abel = A, Bruno = B, Caio = C, e Daniel = D, temos: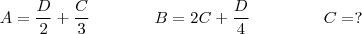 Pelo enunciado, temos D = 60 e A = B. Então:
Pelo enunciado, temos D = 60 e A = B. Então: 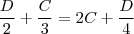 Substituindo:
Substituindo: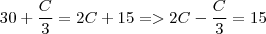 Por mmc, obtemos:
Por mmc, obtemos: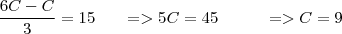
Logo, os quatro amigos possuem, juntos:
33 + 33 + 60 + 9 = 135Alternativa e)
Iniciante escreveu:Considerando: Abel = A, Bruno = B, Caio = C, e Daniel = D, temos: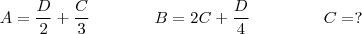 Pelo enunciado, temos D = 60 e A = B. Então:
Pelo enunciado, temos D = 60 e A = B. Então: 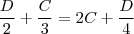 Substituindo:
Substituindo: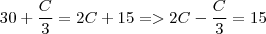 Por mmc, obtemos:
Por mmc, obtemos: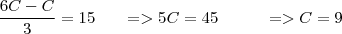
Logo, os quatro amigos possuem, juntos:
33 + 33 + 60 + 9 = 135Alternativa e)
Valeu !
-
israel jonatas
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Mar 14, 2013 13:04
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Conjuntos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Conjuntos] Confusão em teoria dos conjuntos numa questão.
 por Debora Bruna » Seg Jan 11, 2016 17:44
por Debora Bruna » Seg Jan 11, 2016 17:44
- 1 Respostas
- 8842 Exibições
- Última mensagem por DanielFerreira

Sáb Jan 23, 2016 16:44
Conjuntos
-
- [Conjuntos] Dúvida sobre conjuntos vazios
por ALPC » Qui Set 18, 2014 18:28
- 5 Respostas
- 6420 Exibições
- Última mensagem por adauto martins

Seg Set 22, 2014 15:44
Conjuntos
-
- [conjuntos]numeros racionais e conjuntos
por fenixxx » Ter Fev 28, 2012 21:35
- 3 Respostas
- 4730 Exibições
- Última mensagem por DanielFerreira

Sex Mar 02, 2012 00:04
Álgebra Elementar
-
- [Conjuntos] Problema de conjuntos com porcentagem
por Tibes » Qui Jan 31, 2013 14:29
- 1 Respostas
- 7958 Exibições
- Última mensagem por young_jedi

Sex Fev 01, 2013 12:39
Conjuntos
-
- [Conjuntos] Conjuntos e geometria plana
por bencz » Dom Mar 03, 2013 12:58
- 3 Respostas
- 11206 Exibições
- Última mensagem por maison_souza

Sex Nov 14, 2014 13:15
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.