 por yuricastilho » Sáb Abr 05, 2014 19:59
por yuricastilho » Sáb Abr 05, 2014 19:59
Seja

calcule os limites:

Não tenho ideia de como começar porque se substituir infnito dará infinito sobre infinito, que é uma indeterminação.
Também não consegui enxergar nenhuma fatoração ou manipulação algrica. Se alguém puder me ajudar, ficarei muito grato.
Editado pela última vez por
yuricastilho em Dom Abr 06, 2014 22:46, em um total de 1 vez.
-
yuricastilho
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sáb Abr 05, 2014 19:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
 por Russman » Dom Abr 06, 2014 01:15
por Russman » Dom Abr 06, 2014 01:15
Exato. Substituindo

o limite calcula

que é uma indeterminação. Ou seja, esse limite é um número um tanto difícil de obter. Porém, vamos manipular a função. Divida o numerador e o denominador por

.
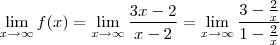
Concorda?
Se sim, basta aplicar o limite. Como

, então
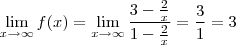
Da mesma forma,
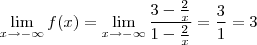
Portanto, a reta

é uma assintota dessa função.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Russman » Dom Abr 06, 2014 01:16
por Russman » Dom Abr 06, 2014 01:16
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por yuricastilho » Dom Abr 06, 2014 22:45
por yuricastilho » Dom Abr 06, 2014 22:45
Muito Obrigado Russman.
Ajudou muito

-
yuricastilho
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sáb Abr 05, 2014 19:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limites] Seja f: R -> R responda:
por yuricastilho » Qui Abr 10, 2014 00:15
- 2 Respostas
- 4846 Exibições
- Última mensagem por yuricastilho

Ter Abr 15, 2014 14:31
Cálculo: Limites, Derivadas e Integrais
-
- (UFC) Seja f a função...
por manuoliveira » Sex Ago 27, 2010 22:20
- 2 Respostas
- 2005 Exibições
- Última mensagem por MarceloFantini

Sáb Ago 28, 2010 17:03
Funções
-
- (ESAL) Seja AB tal que AB= a e AM/MB= 3/5.
por Gustavo R » Sex Ago 12, 2011 21:06
- 2 Respostas
- 1498 Exibições
- Última mensagem por Gustavo R

Sáb Ago 13, 2011 14:49
Geometria Plana
-
- Seja ?(x) uma função derivavel
por kak9 » Ter Out 02, 2018 15:33
- 0 Respostas
- 2984 Exibições
- Última mensagem por kak9

Ter Out 02, 2018 15:33
Cálculo: Limites, Derivadas e Integrais
-
- P.A -Seja ABC um triangulo retangulo
por CrescentMurr » Dom Mar 17, 2013 19:40
- 1 Respostas
- 1769 Exibições
- Última mensagem por young_jedi

Seg Mar 18, 2013 20:19
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 calcule os limites:
calcule os limites:


 o limite calcula
o limite calcula  que é uma indeterminação. Ou seja, esse limite é um número um tanto difícil de obter. Porém, vamos manipular a função. Divida o numerador e o denominador por
que é uma indeterminação. Ou seja, esse limite é um número um tanto difícil de obter. Porém, vamos manipular a função. Divida o numerador e o denominador por  .
.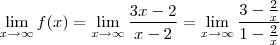
 , então
, então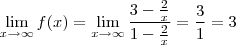
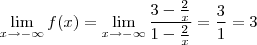
 é uma assintota dessa função.
é uma assintota dessa função.

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.