 por GabriielaCristinaa » Seg Mar 31, 2014 11:23
por GabriielaCristinaa » Seg Mar 31, 2014 11:23
Gostaria de saber se assim como no logaritmo a base do exponencial também não pode ser negativa?
-
GabriielaCristinaa
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Mar 31, 2014 11:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Cleyson007 » Seg Mar 31, 2014 14:18
por Cleyson007 » Seg Mar 31, 2014 14:18
Boa tarde Gabriela!
A função exponencial é definida somente para base a positiva, uma vez que se

é negativo teríamos valores da imagem
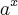
não pertencente ao conjunto dos números reais. Por exemplo para a = -2 e x = 1/2,
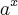
é igual à raiz quadrada de -2 (ver a propriedade P7 do artigo sobre Radiciação ), que pertence ao conjunto dos números complexos, contradizendo a definição da função exponencial.
Fonte:
http://www.blogviche.com.br/2006/04/16/ ... onenciais/Bons estudos.
Qualquer dúvida estou a disposição

Abraço,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por GabriielaCristinaa » Ter Abr 01, 2014 10:45
por GabriielaCristinaa » Ter Abr 01, 2014 10:45
Obrigada! (:
-
GabriielaCristinaa
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Mar 31, 2014 11:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 é negativo teríamos valores da imagem
é negativo teríamos valores da imagem 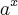 não pertencente ao conjunto dos números reais. Por exemplo para a = -2 e x = 1/2,
não pertencente ao conjunto dos números reais. Por exemplo para a = -2 e x = 1/2, 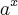 é igual à raiz quadrada de -2 (ver a propriedade P7 do artigo sobre Radiciação ), que pertence ao conjunto dos números complexos, contradizendo a definição da função exponencial.
é igual à raiz quadrada de -2 (ver a propriedade P7 do artigo sobre Radiciação ), que pertence ao conjunto dos números complexos, contradizendo a definição da função exponencial.


