- Considere uma superfície esférica de raio . Determine a área que é removida dessa superfície por um cone com vértice no centro da esfera, se, no vértice, a seção meridiana do cone tem um ângulo de 2? radianos.
Alguém poderia me ajudar nessa questão, seria de grande ajuda!
E um esboço feito: http://sketchtoy.com/59910201
Eu fiz achando a equação do cone, agora estou na duvida. Eu acho a equação (área do cone) e integro ou tenho achar também a área da circunferência?
Quem seria a altura do cone.
O volume de um sólido por revolução é dado pela função V =??[f(x)]²dx
V= ?r²h
V= ?a²h
Quem seria h?
Me ajudem, n sei como resolver essa questão


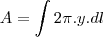
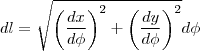

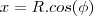
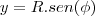
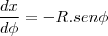
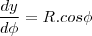


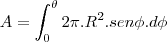
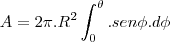

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)