 por marinalcd » Ter Fev 25, 2014 22:46
por marinalcd » Ter Fev 25, 2014 22:46
Preciso mostrar que
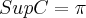
, sendo
![C = [- \sqrt[]{2}, \pi) \cap Q C = [- \sqrt[]{2}, \pi) \cap Q](/latexrender/pictures/ae84012ee4c9cf38effdf4a483b82090.png)
.
Tentei fazer o seguinte:
Defini um
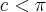
e 1º: somei

nos dois lados e dividi por 2. 2º: somei c nos dois lados e dividi por 2.
Compara as duas desigualdades e cheguei em
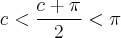
.
O problema é que não posso utilizar esse método, pois tem o número irracional no meio.
Mas não estou conseguindo provar de outra forma.
Alguém pode me ajudar nesse problema?
-
marinalcd
- Colaborador Voluntário

-
- Mensagens: 143
- Registrado em: Sex Abr 27, 2012 21:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por Bravim » Qua Fev 26, 2014 19:56
por Bravim » Qua Fev 26, 2014 19:56
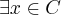
tal que
![-\sqrt[]{2}\leq x < \pi -\sqrt[]{2}\leq x < \pi](/latexrender/pictures/a329b5ad04b53c3686ff4be144a6f9c4.png)
.
![-\sqrt[]{2}-x\leq 0 < \pi - x -\sqrt[]{2}-x\leq 0 < \pi - x](/latexrender/pictures/880c72df55240912dc701fa377e1130a.png)
.
Definindo

tal que
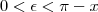
.

.
Agora supomos que exista um supremo para esse conjunto:
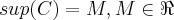
Neste caso,
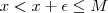
Como devemos escolher o menor limitante superior para esse conjunto,
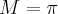
-

Bravim
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Qui Out 03, 2013 03:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
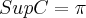 , sendo
, sendo ![C = [- \sqrt[]{2}, \pi) \cap Q C = [- \sqrt[]{2}, \pi) \cap Q](/latexrender/pictures/ae84012ee4c9cf38effdf4a483b82090.png) .
.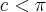 e 1º: somei
e 1º: somei  nos dois lados e dividi por 2. 2º: somei c nos dois lados e dividi por 2.
nos dois lados e dividi por 2. 2º: somei c nos dois lados e dividi por 2.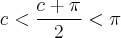 .
.

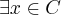 tal que
tal que ![-\sqrt[]{2}\leq x < \pi -\sqrt[]{2}\leq x < \pi](/latexrender/pictures/a329b5ad04b53c3686ff4be144a6f9c4.png) .
.![-\sqrt[]{2}-x\leq 0 < \pi - x -\sqrt[]{2}-x\leq 0 < \pi - x](/latexrender/pictures/880c72df55240912dc701fa377e1130a.png) .
. tal que
tal que 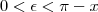 .
. .
.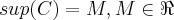
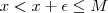
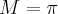


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
