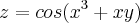.Bom, no começo estava dando certo, derivei tudo em relação x, y.
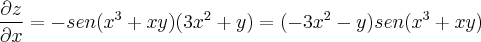
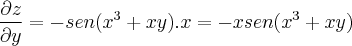
Aí na hora de derivá-los na segunda ordem, o meu resultado deu:
![\frac{\partial^2 z}{\partial x^2} = -6xsen(x^3 +xy) + (-3x^2 - y)[cos(x^3+xy)(3x^2+y)]](/latexrender/pictures/793d6b3d84fdd92a681f135258a2e50c.png "\frac{\partial^2 z}{\partial x^2} = -6xsen(x^3 +xy) + (-3x^2 - y)[cos(x^3+xy)(3x^2+y)]")
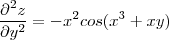
Só que em relação ao x, o gabarito deu
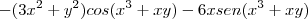, está bem diferente da minha pelo simples fato do termo 
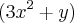aparecer uma vez só no cosseno, o meu apareceu duas vezes, será que eu errei alguma coisa, de sinal, ou algo do tipo? Eu verifiquei tudo de novo, mas deu mesma coisa. Só em relação ao y é que o gabarito correspondeu a minha resposta.Bom, espero que tenham compreendido a minha dúvida, e obrigado!
Abraço!
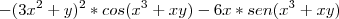? , assim sua resposta bateria com o gabarito.
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.