 por brunnkpol » Sáb Fev 15, 2014 22:16
por brunnkpol » Sáb Fev 15, 2014 22:16
Não tenho a mínima noção de cálculo, mas pelo que eu vi acho que pra essa equação é necessário. Como posso resolver
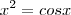
-
brunnkpol
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Ter Mai 07, 2013 16:31
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Dom Fev 16, 2014 22:04
por e8group » Dom Fev 16, 2014 22:04
Acho que tecnicas de análise numérica ajudará você .
Já tentou o método de Newton ? Pesquisando este exercício , encontrei a seguinte solução proposta que emprega M.Newton
http://answers.yahoo.com/question/index ... 542AAFhPRd
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por brunnkpol » Ter Fev 18, 2014 12:19
por brunnkpol » Ter Fev 18, 2014 12:19
Obrigado pela sugestão. Usando o método de newton, achei o valor, mas apenas o positivo. O gráfico (pelo programa de computador) mostra que as funções se interceptam no mesmo valor tanto negativo quanto positivo de x. Outra dúvida é se existe algum meio que eu possa descobrir simplesmente em quantos pontos uma função intercepta a outra.
-
brunnkpol
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Ter Mai 07, 2013 16:31
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Sex Fev 21, 2014 12:31
por e8group » Sex Fev 21, 2014 12:31
brunnkpol escreveu:Obrigado pela sugestão. Usando o método de newton, achei o valor, mas apenas o positivo. O gráfico (pelo programa de computador) mostra que as funções se interceptam no mesmo valor tanto negativo quanto positivo de x
Perfeito !Se pelo metodo de Newton encontrasse ,digamos
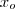
, um valor aproximado para a raiz positiva da eq. dada , ent'ao
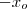
eh uma aproximacao para a raiz negativa da eq . Isto ocorre pq a funcao cosseno e a definida por x(ao quadrado) sao pares.
Desculpe estou com problemas no teclado .
brunnkpol escreveu:Outra dúvida é se existe algum meio que eu possa descobrir simplesmente em quantos pontos uma função intercepta a outra.
Nao sei se ha um metodo especifico . Talvez o TVI ajude . Por exemplo , dadas as funcoes f e g reais , defina h = f-g . Se a funcao h e continua em um intervalo da forma [a,b] e h(a)h(b) < 0 entao pelo TVI existe pelo menos um um numero c entre a e b tal que h(c) = 0 .Mas isto nao nos garanti a quantidade de c presente neste intervalo ,podemos entao reduzir o intervalo usando a metodo da bissecao e verificar se a imagem da funcao oscila o sinal no novo subintervalo e assim por diante .
Tambem podemos verificar se a derivada da funcao eh positiva ou negativa no intrevalo [a,b] , se isto ocorrer juntamente com h(a)h(b) < 0, entao a funcao h possui apenas uma raiz neste intervalo .
Nao sei se estou abilitado para ajudar , mencionei um pouco sobre analise numerica , mas ainda nao estudei tal .Talvez outro membro possa contribuir .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calculo 3 duvida
por robprudente » Qui Fev 12, 2015 13:00
- 1 Respostas
- 1230 Exibições
- Última mensagem por Russman

Qui Fev 12, 2015 20:41
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo 3 - Dúvida
por pedro22132938 » Qui Nov 03, 2016 15:54
- 0 Respostas
- 2814 Exibições
- Última mensagem por pedro22132938

Qui Nov 03, 2016 15:54
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida de calculo iv
 por Raphaelphtp » Seg Jan 16, 2017 15:36
por Raphaelphtp » Seg Jan 16, 2017 15:36
- 0 Respostas
- 689 Exibições
- Última mensagem por Raphaelphtp

Seg Jan 16, 2017 15:36
Cálculo: Limites, Derivadas e Integrais
-
- duvida em calculo de limites
por Andersonborges » Dom Abr 03, 2011 20:13
- 7 Respostas
- 5049 Exibições
- Última mensagem por Guill

Dom Abr 08, 2012 17:07
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida - cálculo de ângulos
por Danilo » Seg Jul 16, 2012 17:23
- 5 Respostas
- 2407 Exibições
- Última mensagem por Arkanus Darondra

Seg Jul 16, 2012 20:59
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
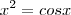


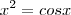



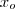 , um valor aproximado para a raiz positiva da eq. dada , ent'ao
, um valor aproximado para a raiz positiva da eq. dada , ent'ao 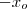 eh uma aproximacao para a raiz negativa da eq . Isto ocorre pq a funcao cosseno e a definida por x(ao quadrado) sao pares.
eh uma aproximacao para a raiz negativa da eq . Isto ocorre pq a funcao cosseno e a definida por x(ao quadrado) sao pares.





