 por Negte » Qui Fev 06, 2014 17:50
por Negte » Qui Fev 06, 2014 17:50
Vestibulinho.
Não consigo resolver na teoria.
Existem 2 torneiras, para encher um tanque vazio. se apenas a primeira fosse aberta por completo,levaria 24 hrs. para encher um tanque.
E se apenas a segunda fosse aberta por completo levaria 48 hrs. para encher o mesmo tanque.
Se eu abrisse as duas juntas....... quanto tempo levaria para encher o tanque?
A)12
B)30
C)20
D)24
*E)16
-
Negte
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qui Jan 02, 2014 12:33
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Mecânica
- Andamento: formado
 por Russman » Qui Fev 06, 2014 18:22
por Russman » Qui Fev 06, 2014 18:22
Comece identificando as vazões de cada torneira. Supondo-as independentes do tempo, podemos escrever
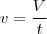
onde

é a vazão e
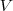
o volume preenchido no tempo

.
Assim, as vazões são , respectivamente,
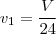
e
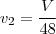
.
Agora, como as torneiras serão abertas simultaneamente, deverão funcionar como uma única de vazão
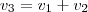
. Assim,
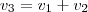
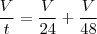
Simplificando
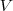
, temos que o tempo

que o tanque será preenchido será tal que
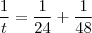
Daí, calculamos
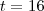
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Negte » Qui Fev 06, 2014 18:30
por Negte » Qui Fev 06, 2014 18:30
Russman escreveu:Comece identificando as vazões de cada torneira. Supondo-as independentes do tempo, podemos escrever
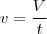
onde

é a vazão e
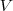
o volume preenchido no tempo

.
Assim, as vazões são , respectivamente,
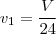
e
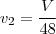
.
Agora, como as torneiras serão abertas simultaneamente, deverão funcionar como uma única de vazão
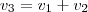
. Assim,
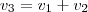
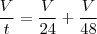
Simplificando
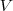
, temos que o tempo

que o tanque será preenchido será tal que
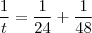
Daí, calculamos
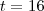
.
obrigado
-
Negte
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qui Jan 02, 2014 12:33
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Mecânica
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [LÓGICA] Sei que tá certo, mas não consigo provar
por v0xxx » Sáb Dez 10, 2011 13:13
- 2 Respostas
- 1348 Exibições
- Última mensagem por v0xxx

Dom Dez 11, 2011 17:18
Álgebra Elementar
-
- [Combinações] Aplicação prática
por Gustavo Gomes » Ter Dez 04, 2012 22:52
- 1 Respostas
- 2306 Exibições
- Última mensagem por young_jedi

Qua Dez 05, 2012 12:28
Análise Combinatória
-
- [Sistemas Matriciais] Atividade Prática
por 13_two » Dom Mai 11, 2014 16:50
- 0 Respostas
- 1461 Exibições
- Última mensagem por 13_two

Dom Mai 11, 2014 16:50
Álgebra Linear
-
- [Dúvida Prática Equações] por favor alguem me responda logo.
por ArthurMoreira » Ter Fev 12, 2013 15:52
- 3 Respostas
- 1523 Exibições
- Última mensagem por DanielFerreira

Ter Fev 12, 2013 17:28
Equações
-
- [LÓGICA] simplificação lógica e leis de equivalência
por MatheusComp606 » Qua Ago 24, 2016 16:13
- 1 Respostas
- 5809 Exibições
- Última mensagem por adauto martins

Seg Ago 29, 2016 15:34
Lógica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


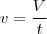
 é a vazão e
é a vazão e 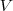 o volume preenchido no tempo
o volume preenchido no tempo  .
.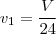 e
e 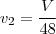 .
.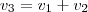 . Assim,
. Assim, 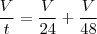
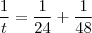
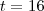 .
.
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.