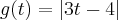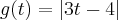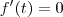Números Críticos

por **Cleyson007** » Ter Jan 28, 2014 18:42

Encontre os números críticos da função $g(t)=\left|3t-4 \right|$ .

por **Man Utd** » Ter Jan 28, 2014 19:44

Como sabemos da teoria que no ponto crítico a derivada é f'(t)=0

ou a derivada não existe.

Veja o gráfico da função g(t)=3t-4

:

agora veja o gráfico da função : g(t)=|3t-4|

:

: Forum ajudmatematica 2.png (11.68 KiB) Exibido 2620 vezes

A função modular rebate a parte negativa da função, e veja que justamente depois da raiz de g(t)=3t-4

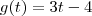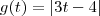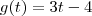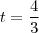que é $t=\frac{4}{3}$ a função assume valores negativos, então a função modular rebate esta parte negativa formando uma espécie de "bico" .Nesse "bico" a função não é derivavél, se quiser confimar vc pode derivar pela definição: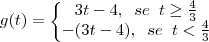

Sabemos que a função módulo, é uma função definida por partes:

$g(t)=\left\{\begin{matrix} 3t-4, \;\; se \;\; t \geq \frac{4}{3} \\ -(3t-4), \;\; se \;\; t<\frac{4}{3} \\ \end{matrix}\right.$

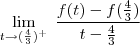
$\lim_{ t \rightarrow (\frac{4}{3})^{+}} \; \frac{f(t)-f(\frac{4}{3})}{t-\frac{4}{3}}$

$\lim_{ t \rightarrow (\frac{4}{3})^{-}} \; \frac{f(t)-f(\frac{4}{3})}{t-\frac{4}{3}}$

por **Cleyson007** » Ter Jan 28, 2014 20:00

Bom, havia pensado da seguinte forma:

$g(t)=\left\{\begin{matrix} 3t-4,\,se\,3t-4\geq 0 & \\ -(3t-4),\,se\,3t-4< 0& \end{matrix}\right.$

Sei também que a deriada da primeira linha dará 3 e da segunda linha dará -3, mas não conclui o raciocínio.

por **Russman** » Ter Jan 28, 2014 23:16

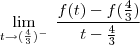
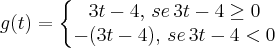
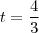O ponto crítico é em $t=\frac{4}{3}$ pois neste a derivada não se define e este ponto pertence ao domínio de g(t)

.

por **Man Utd** » Qua Jan 29, 2014 00:19

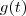Cleyson007 escreveu:Bom, havia pensado da seguinte forma:

$g(t)=\left\{\begin{matrix} 3t-4,\,se\,3t-4\geq 0 & \\ -(3t-4),\,se\,3t-4< 0& \end{matrix}\right.$

Sei também que a deriada da primeira linha dará 3 e da segunda linha dará -3, mas não conclui o raciocínio.

Vc fez a derivada em qual ponto ?

por **Cleyson007** » Qua Jan 29, 2014 08:11

Man Utd e Russman, estou pensando da seguinte forma:

A derivada de g é representada com o intervalo aberto, logo a derivada não está definida no ponto t = 4/3 que é o ponto crítico.

Números Críticos

Números Críticos

Números Críticos

Re: Números Críticos

Re: Números Críticos

Re: Números Críticos

Re: Números Críticos

Re: Números Críticos

Quem está online