Olá, pessoal!
Na questão:
As grandezas G, A, B, C se relacionam da seguinte forma: G é diretamente proporcional a A e a B e é inversamente proporcional a C.
Para A = 8, B = 35 e C = 40, tem-se G = 15.
Então para A = 14, B = 36 e C = 45, qual é o valor de G?
A resposta é 24.
Tentei escrever as grandezas na forma de razões, não cheguei no resultado.... também calculei as variações de cada grandeza e procurei trabalhar com esse índice, sem sucesso....
Aguardo. Grato.


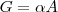
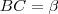
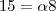
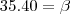



 , avisa que eu resolvo.
, avisa que eu resolvo.

