 por Cleyson007 » Dom Jan 12, 2014 17:11
por Cleyson007 » Dom Jan 12, 2014 17:11
Se um tanque tem 5000 galões de água, que escoa pelo fundo em 40 minutos, então a Lei de Torricelli dá o volume
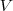
de água que restou no tanque depois de

minutos como
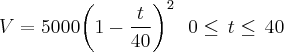
Encontre a taxa segundo a qual a água está escoando do tanque depois de(a) 5 min (b) 10 min (c) 20 min e (d) 40 min. Em que instante o escoamento é mais rápido? E mais vagaroso? Resuma o que você encontrou.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Guilherme Pimentel » Seg Jan 13, 2014 22:43
por Guilherme Pimentel » Seg Jan 13, 2014 22:43
Para ajudar um pouco:
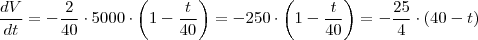
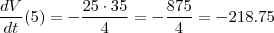
Editado pela última vez por
Guilherme Pimentel em Qua Jan 15, 2014 04:51, em um total de 1 vez.
-
Guilherme Pimentel
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Dom Jan 12, 2014 19:17
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática/Economia
- Andamento: formado
 por Cleyson007 » Ter Jan 14, 2014 00:36
por Cleyson007 » Ter Jan 14, 2014 00:36
Olá, boa noite Guilherme!
Amigo, consegui encontrar os valores para 5min, 10min, 20min e 40min. Estou com dúvida nessa parte: "Em que instante o escoamento é mais rápido? E mais vagaroso? Resuma o que você encontrou."
Pode me ajudar?
Abraço
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Guilherme Pimentel » Qua Jan 15, 2014 04:55
por Guilherme Pimentel » Qua Jan 15, 2014 04:55
Se a pergunta é sobre os tempos nos quais vc calculou a derivada é só comparar os valores obtidos, o de maior valor absoluto é o mais rápido, o de menor valor absoluto é o mais lento.
Se for em relação a todos os momentos possíveis, a resposta é mais rápido em t=0 mais lento em t=40.
-
Guilherme Pimentel
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Dom Jan 12, 2014 19:17
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática/Economia
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
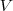 de água que restou no tanque depois de
de água que restou no tanque depois de  minutos como
minutos como 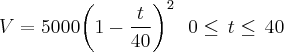



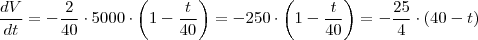
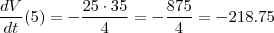

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.