Olá, pessoal! Não estou conseguindo resolver o seguinte exercício:
Obtenha o simétrico do ponto P em relação ao plano:
P=(1,4,2); ?:x-y+z-2=0
Por favor, pode ser só uma dica. Já tentei resolver várias vezes, mas não consigo.
Obrigada!



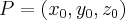 um ponto do plano
um ponto do plano  e
e 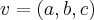 um vetor ortogonal a
um vetor ortogonal a  , a equação geral do plano
, a equação geral do plano  é definida como
é definida como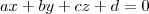 , onde
, onde 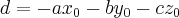
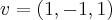
 que passa pelo ponto
que passa pelo ponto 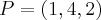 , e como o ponto simétrico a P está contido nessa reta, ele pode ser escrito como
, e como o ponto simétrico a P está contido nessa reta, ele pode ser escrito como 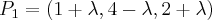 (Verifique!).
(Verifique!). tal que a distância do ponto P ao plano
tal que a distância do ponto P ao plano  seja igual a distância do ponto P1 ao plano
seja igual a distância do ponto P1 ao plano  .
.

 . Mas note o modo como essa reta em particular foi obtida. Inicialmente tomamos um vetor ortogonal ao plano que foi dado pela própria equação geral do plano
. Mas note o modo como essa reta em particular foi obtida. Inicialmente tomamos um vetor ortogonal ao plano que foi dado pela própria equação geral do plano 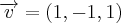 , daí encontramos a reta ortogonal a
, daí encontramos a reta ortogonal a  que tem como vetor diretor o vetor
que tem como vetor diretor o vetor 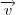 , e que passa pelo ponto P
, e que passa pelo ponto P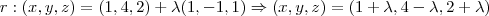




Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante


 , avisa que eu resolvo.
, avisa que eu resolvo.

