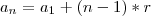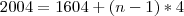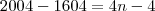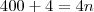Bernar escreveu:São bissextos todos os anos múltiplos de 4 e não múltiplos de 100;
• Também são bissextos todos os anos múltiplos de 400;
• Não são bissextos todos os demais anos.
Sabendo que o ano de 1600 é bissexto, pode-se afirmar que entre 1601 e 2007 ocorreram:
(A) 97 anos bissextos
(B) 98 anos bissextos
(C) 99 anos bissextos
(D) 100 anos bissextos
(E) 101 anos bissextos
Boa tarde, Bernar.
Note que essa sequencia de anos que queremos torna-se uma PA, de razão 4. Além disso temos que
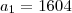
(que é o primeiro ano bissexto no intervalo) e
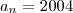
(que é o último ano bissexto no intervalo). Sendo assim:
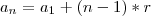
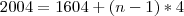
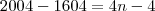
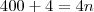

Ou seja, há 101 anos no intervalo que seriam bissextos. Porém, temos que analisar os outros 2 itens:
São bissextos todos os não múltiplos de 100;Nesse caso 1700, 1800, 1900 e 2000 não fariam parte e seriam 'sacados' da nossa contagem, mas pelo outro critério (
Também são bissextos todos os anos múltiplos de 400) temos que o 2000 é bissexto. Sendo assim, só iremos tirar dos 101, três anos.
Resposta: 98.


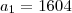 (que é o primeiro ano bissexto no intervalo) e
(que é o primeiro ano bissexto no intervalo) e 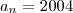 (que é o último ano bissexto no intervalo). Sendo assim:
(que é o último ano bissexto no intervalo). Sendo assim: