Boa noite!
Na primeira questão vc pode iniciar observando que N(t)=2M(t), o que resulta na seguinte equação,
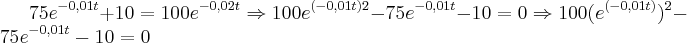
daí faça uma substituição de variável do tipo
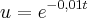
e ficará com uma equação de segundo grau na
variável u, daí para frente é apenas conta, deixo pra vc terminar, vai encontrar um valor de aproximadamente 14,44.
Na segunda questão note que:
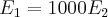
e o valor que deve-se obter é
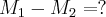
Agora observe que,
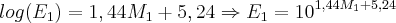
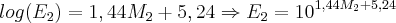
Agora aplicando a iguadade
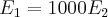
temos,
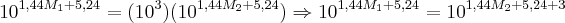
Logo, para encontrar M1-M2 basta passar ambos para o mesmo lado da equação, daí pra frente é só conta, meu resultado deu aproximadamente 2,08.




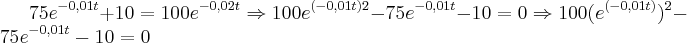
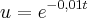 e ficará com uma equação de segundo grau na
e ficará com uma equação de segundo grau na 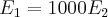
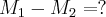
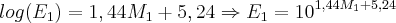
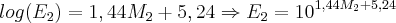
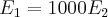 temos,
temos,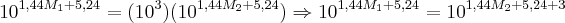




 , avisa que eu resolvo.
, avisa que eu resolvo.

