 por Pessoa Estranha » Sáb Dez 28, 2013 15:45
por Pessoa Estranha » Sáb Dez 28, 2013 15:45
Pessoal, estou com o exercício de um trabalho de Cálculo I para resolver, mas acho que a minha resposta está errada. Por favor, ajudem!
"Calcule a área da região limitada pela curva
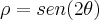
."
Deve-se trabalhar em coordenadas polares.
Não quero a resolução. Gostaria apenas de saber a resposta correta. A minha é
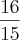
.
Obrigada!
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Man Utd » Dom Dez 29, 2013 16:53
por Man Utd » Dom Dez 29, 2013 16:53
Olá

não está correto, de acordo com os meus cálculos o resultado certo é

-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por Pessoa Estranha » Seg Dez 30, 2013 09:19
por Pessoa Estranha » Seg Dez 30, 2013 09:19
Obrigada por responder!
Bem, vou tentar fazer novamente.

-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Pessoa Estranha » Qui Jan 02, 2014 21:44
por Pessoa Estranha » Qui Jan 02, 2014 21:44
Olá!
Só agora voltei neste exercício e, o meu resultado foi

. Aplicando a integral, realmente chega-se a

, mas quando apliquei a fórmula para as coordenadas polares, deu resultado diferente.
Ainda estou errada ?
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Man Utd » Sex Jan 03, 2014 17:24
por Man Utd » Sex Jan 03, 2014 17:24
Pessoa Estranha escreveu:Olá!
Só agora voltei neste exercício e, o meu resultado foi

. Aplicando a integral, realmente chega-se a

, mas quando apliquei a fórmula para as coordenadas polares, deu resultado diferente.
Ainda estou errada ?
Vc está certa o resultado é msm

, foi mal pelo engano

.
calculando a área de um laço e multiplicando por 4 obtemos a resposta:

-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- calculo do VAL - exercício
por nhrd » Qui Dez 11, 2008 23:40
- 0 Respostas
- 3666 Exibições
- Última mensagem por nhrd

Qui Dez 11, 2008 23:40
Matemática Financeira
-
- Cálculo em exercício
por Sofiaxavier » Ter Out 19, 2010 20:08
- 1 Respostas
- 1361 Exibições
- Última mensagem por MarceloFantini

Ter Out 19, 2010 20:32
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo] Exercício
por Pessoa Estranha » Sex Nov 15, 2013 10:26
- 5 Respostas
- 2404 Exibições
- Última mensagem por Pessoa Estranha

Sex Nov 15, 2013 17:08
Cálculo: Limites, Derivadas e Integrais
-
- Exercício calculo III
 por HenriqueGS » Dom Jun 05, 2016 20:27
por HenriqueGS » Dom Jun 05, 2016 20:27
- 3 Respostas
- 3690 Exibições
- Última mensagem por DanielFerreira

Sáb Jun 11, 2016 08:42
Cálculo: Limites, Derivadas e Integrais
-
- Exercicio Calculo 3
por leocr » Qua Set 20, 2017 11:16
- 0 Respostas
- 2059 Exibições
- Última mensagem por leocr

Qua Set 20, 2017 11:16
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
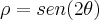 ."
."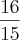 .
.
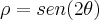 ."
."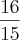 .
.





 . Aplicando a integral, realmente chega-se a
. Aplicando a integral, realmente chega-se a  , mas quando apliquei a fórmula para as coordenadas polares, deu resultado diferente.
, mas quando apliquei a fórmula para as coordenadas polares, deu resultado diferente.
. Aplicando a integral, realmente chega-se a
, mas quando apliquei a fórmula para as coordenadas polares, deu resultado diferente.
 , foi mal pelo engano
, foi mal pelo engano  .
.




 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.