Escreva as perdas sucessivas em uma progressão:
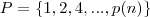
onde
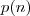
é o valor perdido na nº rodada.
Note que ao fim da 1º rodada ele perde 1 real. Ao fim da 2º perdeu 1+2 = 3 reais. Ao fim da 3º perdeu 1+2+4 = 6 reais. Ao fim da... e assim sucessivamente.
Portanto, ao fim da nº rodada ele terá perdido a SOMA de todas perdas anteriores. Portanto, você procura um número

tal que
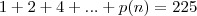
pois 225 é a perda total.
A progressão citada identificamos como uma progressão geométrica. Portanto, calcule o temro geral
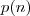
, aplique na fórmula da soma dos n primeiros termos e iguale a 225. Assim, você obterá uma equação em n e , com a solução, terá o número de rodadas a qual ele perdeu 225 reais. Que jogador ruim, né?


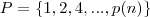
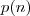 é o valor perdido na nº rodada.
é o valor perdido na nº rodada. tal que
tal que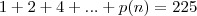

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.