por vanu » Dom Dez 15, 2013 15:20
calcular o comprimento do arco dado por x=1/2. y³(ao cubo)+1/6y³(ao cubo)-1 sendo que 1<=Y<=3
eu sei que tenho derivar o f'(x) que fica: 3/2.y² -1/6y²
agora utilizando a forma
http://upload.wikimedia.org/math/e/1/d/ ... 9ad941.pngque nao sei fazer a integral alguem pode me ajudar
RESULTADO FINAL E 118/9
-
vanu
- Novo Usuário
-
- Mensagens: 6
- Registrado em: Qua Dez 11, 2013 14:44
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: cursando
por Russman » Dom Dez 15, 2013 15:37
A função é
?
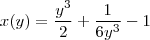
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário
-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral Imprópria
por CrazzyVi » Seg Set 27, 2010 17:13
- 5 Respostas
- 7250 Exibições
- Última mensagem por menino de ouro
Qui Jan 24, 2013 13:43
Cálculo: Limites, Derivadas e Integrais
-
- Integral impropria
por menino de ouro » Dom Jan 13, 2013 17:04
- 3 Respostas
- 2455 Exibições
- Última mensagem por thejotta
Seg Jan 14, 2013 00:11
Cálculo: Limites, Derivadas e Integrais
-
- Integral Imprópria
por Man Utd » Sex Ago 09, 2013 16:09
- 0 Respostas
- 1245 Exibições
- Última mensagem por Man Utd
Sex Ago 09, 2013 16:09
Cálculo: Limites, Derivadas e Integrais
-
- Integral impropria
por vanu » Qui Dez 12, 2013 20:05
- 1 Respostas
- 1411 Exibições
- Última mensagem por Man Utd
Sex Dez 13, 2013 11:22
Cálculo: Limites, Derivadas e Integrais
-
- Integral impropria
por isabelrebelo » Qui Abr 23, 2015 17:24
- 0 Respostas
- 1572 Exibições
- Última mensagem por isabelrebelo
Qui Abr 23, 2015 17:24
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:
Então pense o seguinte: a fração geratriz de 0,05 é
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,
da seguinte forma:
.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,
da seguinte forma:
.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
