 por krath » Seg Dez 09, 2013 16:32
por krath » Seg Dez 09, 2013 16:32
Boa tarde a todos, estou com muita duvida em um exercicio do vestibular da FEI quanto a composicao de Funcoes. La vai
35. Sejam f e g funcoes definidas de IR em IR. Se f(x) = 3x - 1 e fog (x) = 12x + 5, então g(x) é tal que:
a) g(1) = 2
b) g(1) = 3
c) g(1) = 4
d) g(1) = 5
e) g(1) = 6
Minha duvida é o desenvolvimento, eu saberia chegar no fog(x) se me dessem f(x) e g(x) mas nao sei chegar no g(x) tendo o f(x) e o fog(x), ou seja nao sei fazer o caminho "inverso"
Por favor me ajudem
Muito Obrigado!
-
krath
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Nov 22, 2013 02:28
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: estudante
- Andamento: cursando
 por e8group » Seg Dez 09, 2013 17:20
por e8group » Seg Dez 09, 2013 17:20
Suponha que você conheça a regra de associação de

.Então,
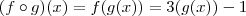
.Por outro lado , sabemos que
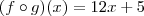
. E daí ,
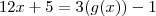
. Agora pode determinar

.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por krath » Ter Dez 10, 2013 11:26
por krath » Ter Dez 10, 2013 11:26
boa cara, consegui fazer gracas a voce. Otima explicacao, mt obrigado!
-
krath
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Nov 22, 2013 02:28
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: estudante
- Andamento: cursando
 por e8group » Qua Dez 11, 2013 13:51
por e8group » Qua Dez 11, 2013 13:51
Não foi nada .Abraços.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Composição de Funções]
por phelipe » Qui Abr 19, 2012 16:09
- 3 Respostas
- 1645 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 21, 2012 13:11
Funções
-
- tábua para a lei de composição interna
 por leticiapires52 » Qua Abr 06, 2016 16:33
por leticiapires52 » Qua Abr 06, 2016 16:33
- 0 Respostas
- 2836 Exibições
- Última mensagem por leticiapires52

Qua Abr 06, 2016 16:33
Álgebra Elementar
-
- [Algebra Linear] - Composição de transformação Linear
por aligames321 » Ter Dez 04, 2012 23:53
- 1 Respostas
- 10530 Exibições
- Última mensagem por young_jedi

Qua Dez 05, 2012 12:45
Álgebra Linear
-
- duvida em funcoes
por bmachado » Qua Fev 29, 2012 00:33
- 2 Respostas
- 1564 Exibições
- Última mensagem por bmachado

Qua Fev 29, 2012 16:51
Funções
-
- Funções Dúvida
 por Louis » Seg Jul 09, 2012 23:56
por Louis » Seg Jul 09, 2012 23:56
- 8 Respostas
- 3708 Exibições
- Última mensagem por e8group

Ter Jul 10, 2012 18:36
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 .Então,
.Então, 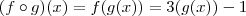 .Por outro lado , sabemos que
.Por outro lado , sabemos que 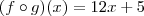 . E daí ,
. E daí , 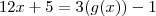 . Agora pode determinar
. Agora pode determinar  .
.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.