 por lanaamonteiro » Seg Dez 09, 2013 11:27
por lanaamonteiro » Seg Dez 09, 2013 11:27
O enunciado da questão diz o seguinte:
"Verificar se o subconjunto de P4 (R) é LI ou LD:
W= {x(x-1), x³, 2x³-x², x}"
Eu tentei resolver da seguinte forma:
>

1*(x²-x) +

2*(x³) +

3*(2x³-x²) +

4*(x)
> (-

1 +

4)*x + (

1 -

3)*x² + (

2 + 2*

3)*x³
|

1 +

4 =0
|

1 -

3 =0
|

2 + 2*

3 =0
Depois daí eu não consigo mais resolver, porque esse sistema não tem solução! :/
também não sei se fiz certo até aí,
por favor ajudem!

Obrigada.
-
lanaamonteiro
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Dez 09, 2013 11:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng Civil
- Andamento: cursando
 por e8group » Seg Dez 09, 2013 12:21
por e8group » Seg Dez 09, 2013 12:21
A princípio parece que este conjunto é L.D. , a cardinalidade do mesmo é 4 que é maior que o grau de qualquer polinômio escrito como combinação linear dos polinômios de W . Definamos
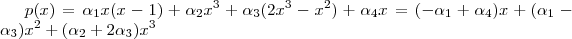
.
.
Se
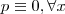
,então
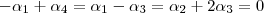
que é um sistema de três equações com 4 incógnitas , como o número de varáveis é maior que o de eq. é natural esperar que teremos algumas incógnitas em funções de outras . Por exemplo , escolhendo
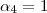
,obteremos
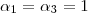
e
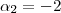
.
Verificando :
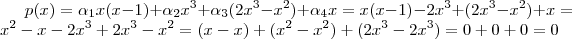
para todo

.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Dependência Linear com Polinômios] Dúvida em exercício
por lanaamonteiro » Seg Dez 09, 2013 11:23
- 1 Respostas
- 1094 Exibições
- Última mensagem por Russman

Seg Dez 09, 2013 22:54
Álgebra Elementar
-
- [Dependência Linear] Exercício do Boulos
por Vinicius Rodrigues » Dom Abr 01, 2012 01:52
- 2 Respostas
- 1256 Exibições
- Última mensagem por Vinicius Rodrigues

Dom Abr 01, 2012 03:43
Geometria Analítica
-
- [DEpendência Linear] Álgebra Linear
por Ronaldobb » Ter Mar 25, 2014 14:22
- 1 Respostas
- 1114 Exibições
- Última mensagem por young_jedi

Qui Mar 27, 2014 00:10
Álgebra Linear
-
- Dependência Linear
por -civil- » Qui Jul 07, 2011 23:19
- 1 Respostas
- 1167 Exibições
- Última mensagem por LuizAquino

Sex Jul 08, 2011 10:55
Geometria Analítica
-
- [GA] Dependência Linear
por Larissa28 » Ter Mar 31, 2015 20:31
- 4 Respostas
- 1775 Exibições
- Última mensagem por Larissa28

Qua Abr 01, 2015 20:19
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 1*(x²-x) +
1*(x²-x) +  2*(x³) +
2*(x³) +  3*(2x³-x²) +
3*(2x³-x²) +  4*(x)
4*(x) 1 +
1 +  4)*x + (
4)*x + (  1 -
1 -  3)*x² + (
3)*x² + (  2 + 2*
2 + 2* 3)*x³
3)*x³ 1 +
1 +  4 =0
4 =0 1 -
1 -  3 =0
3 =0 2 + 2*
2 + 2* 3 =0
3 =0


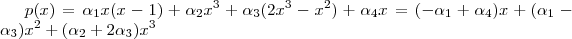 .
. 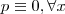 ,então
,então 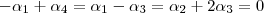 que é um sistema de três equações com 4 incógnitas , como o número de varáveis é maior que o de eq. é natural esperar que teremos algumas incógnitas em funções de outras . Por exemplo , escolhendo
que é um sistema de três equações com 4 incógnitas , como o número de varáveis é maior que o de eq. é natural esperar que teremos algumas incógnitas em funções de outras . Por exemplo , escolhendo 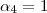 ,obteremos
,obteremos 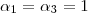 e
e 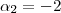 .
.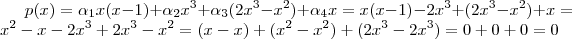
 .
.