Olá gostaria de tirar uma dúvida,vou postara pergunta
Admita dois números inteiros positivos, representados por a e b. Os restos das divisões de a e b por 8 são, respectivamente, 7 e 5.
Determine o resto da divisão do produto a.b por 8.
Eu já vi nesse próprio site como se faz,mas minha duvida ficou na resolução
minha duvida é como montaram essas 2 equações aqui
a = 8.x + 7
b = 8.y + 5
não entendi pq eles pegaram a divisão e multiplicaram para um numero x e somaram com o resto,alguem pode explicar ?


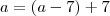 . Dividindo ambos lado da igualdade por
. Dividindo ambos lado da igualdade por  ,
, 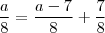 . Utilizando a hipótese do resto da divisão de
. Utilizando a hipótese do resto da divisão de  por
por 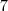 ,segue-se a soma dos restos da divisão de cada número inteiro divididos por
,segue-se a soma dos restos da divisão de cada número inteiro divididos por 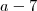 por
por  o que mostrar que o número
o que mostrar que o número 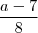 é inteiro . Pondo
é inteiro . Pondo 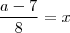 ,resulta
,resulta 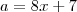 .
.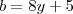 .
.
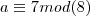
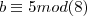
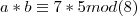
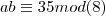
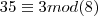 , ficaremos com:
, ficaremos com: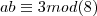
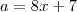 para
para  inteiro! Da mesma forma temos
inteiro! Da mesma forma temos 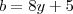 com
com  também inteiro.
também inteiro. obteremos
obteremos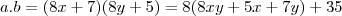
 por
por  . Assim,
. Assim, 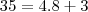 de modo que
de modo que 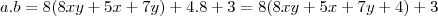
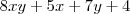 é certamente inteiro também. Chamando este número de
é certamente inteiro também. Chamando este número de 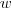 , temos
, temos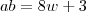 .
.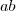 dividido por
dividido por